Infinity is a paradox

Infinity is used on daily basis in Math, especially after the Cantor's work. Here, we try to prove its paradoxical nature. Then try to discuss why this happended to us, as a society who developed, and taught, a false idea over centuries! Hopefully in the future, we could avoid such a mistake.
Above wallpaper reference1
There are a lot of mathematicians who think infinity is nonsense and should not be used in math, and they reconstruct a very big portion of math without using such concept, but they are not a lot, and that's bothering me! For instance, one of the mathematicians who works in this area is Norman Wildberger where you can make yourself familiar with his works by watching his Youtube channel. You can start by
Although I like Wildberger's videos, he's not the only mathematician who think like that! You can find more by studying works that have been done on Finitism2, Constructivism3, and Intuitionistic type theory4. This post is basically about the fact that I'm a fan of them, so it's not adding much to what we already know, but please don't forget to share the reference along with the idea5. I spent some time on it, so here is my thought flow and some proofs that I couldn't see around, but I'm sure because their underlying math is so simple and well-known, someone else have thought about them before.
It tooks a while for people to accept the Cantor's work6, 7. The reason is that they are so sophisticated and beautiful, rare number of mathematicians could resist. However, even if we don't stick to infinity to use those beautiful proofs, we still have Information Theory8, and a lot of other area of science, to apply that beauty, so it's not a good reason to keep infinity around when we know it's full of paradoxes. By looking at the standard math that is teaching in the universities, someone can see when we decrease \( x \), like \( x\rightarrow 0 \), in \( \frac{1}{x} \) function, when \( x = 0 \) we call the result undefined, or \( \infty \), but non of textbooks have problem with real numbers9, \( \mathbb{R} \), in which, based on the Cantor's work, a bigger infinity is laid! Notice, the concept of real numbers was around like 2000-3000 years, so it didn't start by Cantor's work, but Cantor discovered some patterns there less than two centuries ago, therefore, someone can argue that because it's a much older concept, that's why textbooks act more like it's a valid concept.
Real numbers are an older concept, because we can think of them as the continuum of space around us. I like this approach, because, it assumed the reality around us is consistent, so we should be able to define it mathematically and use it in our proofs without worrying about its internal consistency! But after discovery of atoms and molecules, which shows continuum in the matter is not acually a continuum, we didn't update our axioms like a good scientist, who must use Bayesian inference10 to update their prior all the time.
Is math free just because it's not tied to experiment?
The idea that Mathematics is free to study all kind of structures and relations is missleading, because even classically, all mathematical proofs are at least restricted to the boundary of mathematical logic11, but the story of infinity shows we need to restrict it a little bit more to avoid such nonsense in the future.
The power of math is that in a lot of cases they developed theorems that has no application in reality, but the underlying axioms were close enought to the reality and Physics, to envelope those theorems inside and waited to be discovered. Additionally, those theorems stick to the constructivism, even if their developers have no idea about it. A simple example is the Riemannian geometry12 that is developed without any application in Physics, but because it constructively build upon Euclidean geometry13, which is very close to our reality, later Albert Einstein14 found a very valid application of it in the General relativity15.
These kind of things used to amaze me, but nowadays, they look like obvious, because construction on top of observable objects keeps creating valid objects. It's very deep actually! Even building a logical proof is some kind of a construction, so it can gives logic itself its validity. Therefore, it could explain why mathematical logic can make valid statements, if the starting objects are observables or constructed from observable objects.
Also it used to amaze me that a person, Einstein, could make a theory, General relativity15, that was far far away from humanity's knowledge at the time in a way that we could test it a century later with success! But he didn't do his magic just once! He did it in his previous works as well, for instance Special relativity16, where nobody knew about time dilation17 experimentally! When you review his method to discover his thoeries, you notice there's no magic! He just insisted to make them consistent with day to day life. For instance, take a look at his argument against Copenhagen interpretation of Quantum Mechanics18. He called collapsing of an entangled wave function spooky action at the distance, because it's not a constructable process based on what we, the scientists in day to day life observe in the universe. Be aware that this is totally on the opposite direction of claims like "Quantum Mechanics Isn’t Weird, We’re Just Too Big"! It doesn't matter how big or small we're, we should be able to construct our Physics' theories.
Another element that is well-known to us and made Einstein's work consistent is his thought experiments19, which are basically some imagination of construction of a real experiment, but that experiment is never happened! They are just constructable by existing objects, therefore, they exists! Although, most of his thought experiments never tested in reality, their results, which are his theories, are working perfectly in the reality. For instance, he has a thought experiment that he built a clock by using light, two mirrors, and their known relations, which all of them are observables. This clock is never built in reality, but time dilation17 and other properties of the Special relativity16 are derived out of it. This method is what we should learn and teach in universities, but first we need to make it a part of the foundation of mathematics.
The fact that infinity doesn't exist implies there is a max number that we should respect in our calculation, which we already know how to deal with such a system. We call that Modular arithmetic20,so we should replace all usage of ordinary arithmatic21 with the modular one. This move will cure the logic by putting a boundary in first Gödel's incompleteness theorem22 and the latter ones, which means we can talk about a consistent universe in which we can prove its consistency by a handful of axioms. A dream of any mathematician!
Hence looks like
In the philosophy of mathematics, constructivism asserts that it is necessary to find (or "construct") a specific example of a mathematical object in order to prove that an example exists. -- Wikipedia
is a correct, and very useful, principle. It's a very compelling statement for me, because it relies on the fact that mathematics should study observables and their related abstractions, because what exists is consistent as what we seek in the math. Thus if it's such a great tool, why don't we use it all the time in our foundation of mathematics?
Just to make it clear, not using the constructive method would cost us a lot! Let's look at the Copenhagen interpretation18, which at least has one non constructive process, which we know as the measurement problem23. Currently a lot of companies spend a lot of money to build Quantum Computers24, where if you've read my other post, Understanding Quantum Mechanics25, you would know that based on the Resonance interpretation25 they are just analog computers, with a new branding, of course! But they inherently suffer from the same symptoms of other analog computers, which mainly is not being able to reproduce the results, as I discussed in my other post, Reproducibility5. This alone means running them will be very costful! Its consequence is that all those costs will eventually hack the RSA26, with Shor's algorithm27, but will not provide us with any additional Quantum security, which are promissed based on the collapsing process! So we bet against ourselves based on a non-constructive math, which have some wrong promisses! Notice, Shor's algorithm27 will work because even in the Resonance interpretation25, the system will pick a random state among others, which is enough for Shor's algorithm to work, but in this interpretation this process is constructive in a deterministic way, and explained before.
Infinity's paradoxes
As mentioned before there are a lot of inconsistencies and paradoxes when you work with infinity. For instance, Banach–Tarski paradox28, Hilbert's paradox of the Grand Hotel29, etc. Also it's fun to watch
Especially the part starting from 37m:34s. But I could think of more!
Zero probability
Let's start by a simple one. The definition of probability30 based on Wikipedia is
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty.
where to formulate it we can be agree to name the events by the numbers on an axis, \( X \). Then we naturally come up with the definition of probability distribution31. When you draw it, it looks like what you can find in the Wikipedia page of the probability distribution31
So far so good, everything makes sense! But let's expand our definition to continuum of the real numbers like the problem of randomly throwing a dart in a platonic universe32, where infinity exists!

But as soon as applying this innocent improvement, the rules are changing! The behaviour of probability distribution for many random variables with finitely or countably infinitely many values is different from for many random variables with uncountably many values! The former probability distribution is consistent with all we defined previously, and we call it discrete, but for the latter one, we have to work with intervals to get the probability, and we call it continuous. In the formal language of math it goes like this for discrete probability distribuion of event \( E \)
\[ P(X\in E)=\sum_{\omega \in E}P(X=\omega ) \]
but for the continuous one we have to only talk about an interval of events \( E \)
\[ P(X\in E)=\int_{E}f(X)dX \]
This changing behaviour is what we do all the time when we use integral33, hence, it's a very regular change, but in the context of probability distribution this paradoxical change is more bold, therefore, we only talk about this context here. Anyway! By saying a poof! It was close!, we think that we fixed the problems by separating these cases! Nonetheless, in a platonic universe32, where infinity exists, the dart has a continuum curve shape, where its extremum point34 is its head. Thus, the probability of touching the head of the dart to the wall is the probability of that single point, so no interval in the platonic universe is needed! However, based on above recipe, the probability of touching the head of the dart, which is a point, to the wall is zero, because integral of an interval with zero length is zero. Notice, \( P(X\in E) \) supposed to be the same probability that we defined before, disregarding of using discrete or continuous events, which based on the definition of probability 0 indicates impossibility of an event, but touching the head of the dart to the wall is not impossible and it has zero probability! Hm! Let's ignore it and continue our fantasy, right? :D But by definition it's a paradox!
Riemann sphere
Riemann sphere35 is very interesting. Wikipedia's introduction is
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value \( \infty \) for infinity. With the Riemann model, the point \( \infty \) is near to very large numbers, just as the point \( 0 \) is near to very small numbers.
As you can see it's not clear in this definition why it's related to a sphere! But this picture shows why.
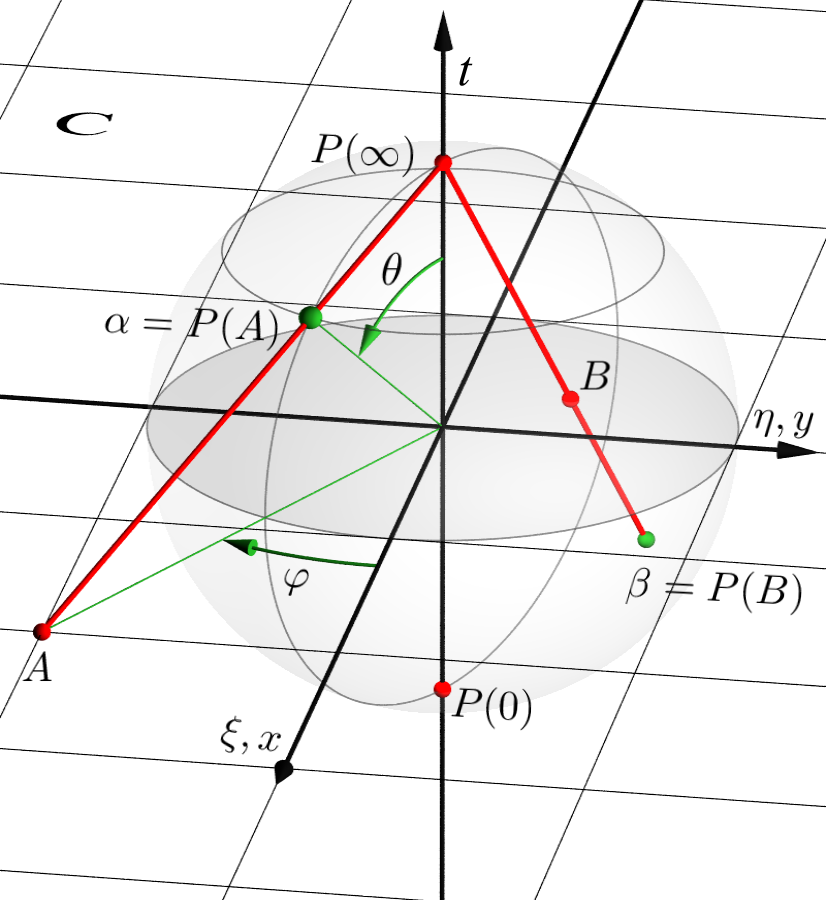
For instance, point \( A \) on the complex plane has a 1-to-1 correspondence36 with point \( \alpha = P(A) \) on the sphere. This bijection36 function, \( P(.) \), is available for all points on the complex plane. It covers all the point on the sphere except the point on the north pole, \( P(\infty) \). It's interesting because it relates the infinity to topology, on one hand, and on the other hand, it gives a funtion that can be used in arguments like Cantor's arguments! Existance of \( P(.) \) shows the cardinality37 of points on the complex plane, where we display it like \( |\mathbb{C}| \), equals to cardinality of point on the sphere except the north pole, where we present it like \( |\mathbb{S^{-}}| \).
\[ |\mathbb{S^{-}}| = |\mathbb{C}| \]
That one point in the north pole, \( P(\infty) \), is creating such a difference that there's no function to make a 1-to-1 correspondence between points on the sphere, \( \mathbb{S} \), and the points on the complex plane, \( \mathbb{C} \), so based on Cantor's method
\[ |\mathbb{S}| \neq |\mathbb{C}| \]
In the same way, we can also argue that there's a function to make a 1-to-1 correspondence between \( \{P(\infty)\} \cup \mathbb{S^{-}} \) and \( \mathbb{S} \), so
\[ |\{P(\infty)\} \cup \mathbb{S^{-}}| = | \mathbb{S} | \neq |\mathbb{C}| \]
Hence, as long as, cardinality is behaving like a number for all finit sets, therefore, we expect we could sum it up with \( 1 \), unless someone come along and says we change the rules whenever we want. Thus, because we know \( |\{P(\infty)\}| = 1 \), then
\[ | \mathbb{S} | = |\{P(\infty)\} \cup \mathbb{S^{-}}| = |\{P(\infty)\}| + |\mathbb{S^{-}}| \]
which means
\[ |\mathbb{S^{-}}| + 1 \neq |\mathbb{S^{-}}| \]
this behaviour contradicts with defined behaviour of infinity, \( \infty = \infty + 1 \)! But don't give up yet! We're clever! Let's think of a number, \( Z \), which satisfies
\[ | \mathbb{S} | = |\{P(\infty)\} \cup \mathbb{S^{-}}| = Z + |\mathbb{S^{-}}| \]
Thus we have
\[ |\mathbb{S^{-}}| + Z \neq |\mathbb{S^{-}}| \]
where \( Z \) can be any real number, plus \( \infty \) itself, but in all cases it has contradiction with the definition of infinity, aka \( \infty = \infty + 1 \), and \( \infty = \infty + \infty \). So being clever didn't work!
By now, I hope it's clear that in a world that infinity exists, aka platonic universe, topology cannot exist in a consitent way! So let's say goodbye to infinity and start an era beyound infinity :P
References
Cite
If you found this work useful, please consider citing:
@misc{hadilq2022Infinity,
author = {{Hadi Lashkari Ghouchani}},
note = {Published electronically at \url{https://hadilq.com/posts/infinity-is-a-paradox/}},
gitlab = {Gitlab source at \href{https://gitlab.com/hadilq/hadilq.gitlab.io/-/blob/main/content/posts/2022-09-13-infinity-is-a-paradox/index.md}},
title = {Infinity is a paradox},
year={2022},
}