Did you ever come to the point to ask yourself what's the Inner product¹ between a vector and a Bivectors²? If you did, you may noticed soon that it doesn't have any meaningful answer yet. I got interested into this problem back when I was studying Mathematical Physics course in my bachelor degree. I wrote my finding to my professor. "wooow! You defined a higher dimensional Levi-Civita-Symbol³", he saied. But my invention was much useful than that! This post is the details of that invention. If you know about vectors, and bivectors, etc. I encourage you to read to the end, because this tool is simple and super useful.

---

Above wallpaper reference¹

At the time, I even didn't know about the Interior product², Exterior algebra³, or Clifford algebra⁴. When I become familiar with these concepts I always wanted to find out somebody get to the point I've got, but it didn't happen yet. However, I would not be surperised if somebody actually found it before, as it happened before to me. For instance, I've found Newton's series with Finite difference⁵, but I didn't know, until years ago, people already knew about it for centuries. Even in that case, it shows that I'm sometime dumb, sometime stupid, but sometime on the cutting edge of human knowledge. Anyway, I hope you and next generations find it a useful and enjoyful tool to work with. Please make the 4D and higher dimensional studio softwares sooner so I could see your awesome animations in my lifetime :D

Also don't forget to reference with the link of this page, because there will be no paper with so called "scientific format", and I can assure you Gitlab, which holds this post, will stay around more than Arxiv, or any so called academic publisher, because it's open source and have a bussiness model!

Before going to the new stuff let's review what we already know. Assume a \( 3D \) Euclidean space⁶, where we define the Inner product of two vectors, \( \vec A \), and \( \vec B \), on \( \hat x \), \( \hat y \), and \( \hat z \) basis,

\[ \vec A = a_x \hat x + a_y \hat y + a_z \hat z\\ \vec B = b_x \hat x + b_y \hat y + b_z \hat z \]

like this:

\[ \vec A.\vec B = a_x b_x + a_y b_y + a_z b_z. \]

Until now it's just a definition, but after some theorems we can prove that there's a geometric interpretation for this definition. It looks like magic, but the main purpose of this post is to extend this magic to the higher dimension.

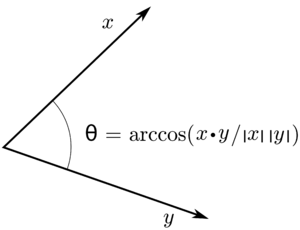The angle between \( x \) and \( y \) vectors is \( \theta \).

Now it's the time for investigating the Cross product⁷ as well. For the same vectors \( \vec A \), and \( \vec B \) above, we have:

\[ \vec A \times \vec B = (a_y b_z - a_z b_y)\hat x - (a_x b_z - a_z b_x)\hat y + (a_x b_y - a_y b_x)\hat z \]

which after proving some theorems we can find its geometric interpretation as shown in this image:

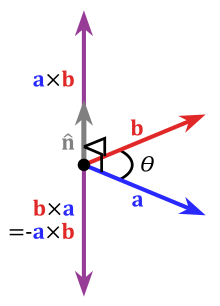The result of cross product between \( a \), and \( b \) vectors.

along with this magical formula:

\[ \left| \vec A \times \vec B \right| = \left| \vec A \right| \left| \vec B \right| \sin (\theta) \]

where \( \theta \) is the angle between \( \vec A \) and \( \vec B \). Notice we used the definition of norm⁸ above like this: \( {\left| \vec A \right|}^2 = \vec A.\vec A \). But as you may know the Cross product is not scalable to more than \( 3D \) spaces. The next best thing to describe the product of two vectors in higher dimensions, which can describe a surface, is a bivector⁹. It's also scalable for multi-vector products, which can describe \( 3D \)-surface, etc. on higher dimensional spaces. Does a \(3D\)-surface make sense to you? It makes sense to me! It's just a \(3D\) object floating in the higher dimensional spaces. To start we need to simplify above notation. Let's have basis like \( \mathbf{e}_i \), where \( i \) can change from \( 1 \) to \( 3 \), where \( 3 \) is the dimensionality of our space. Therefore we have

\[ \mathbf{A} = a_1 \mathbf{e}_1 + a_2 \mathbf{e}_2 + a_3 \mathbf{e}_3\\ \mathbf{B} = b_1 \mathbf{e}_1 + b_2 \mathbf{e}_2 + b_3 \mathbf{e}_3. \]

Now we can define wedge product³ with anti-symmetric and linear properties:

\[ \mathbf{A}\wedge \mathbf{B} = - \mathbf{B}\wedge \mathbf{A} \]

thus, we can conclude

\[ \mathbf{A}\wedge \mathbf{B} = \left(a_1 \mathbf{e}_1 + a_2 \mathbf{e}_2 + a_3 \mathbf{e}_3\right)\wedge \left( b_1 \mathbf{e}_1 + b_2 \mathbf{e}_2 + b_3 \mathbf{e}_3\right) = \\ (a_2 b_3 - a_3 b_2)\mathbf{e}_2 \wedge \mathbf{e}_3 - (a_1 b_3 - a_3 b_1)\mathbf{e}_3\wedge\mathbf{e}_1 + (a_1 b_2 - a_2 b_1)\mathbf{e}_1\wedge\mathbf{e}_2. \]

We'll call this a 2-vector, which is the description of a surface on a finite-dimensionsional space. The generalization of the concept of totally anti-symmetric property of the wedge product will lead to k-vector. The space of all k-vector will be denoted by \(\bigwedge\nolimits^k\left(V\right)\).

Look how above 2-vector is similar to the Cross product. In fact, you can interpret it the same way as what we had for the Cross product.

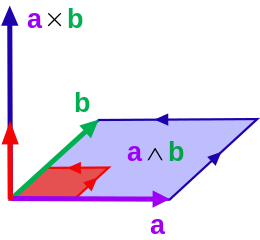
To regularize this relationship we need to define Hodge duality¹⁰, and Interior product², etc. which is not how I found these concepts. Nonetheless, that approach is so confusing, because you need to define the Dual space¹¹, then the Interior product, then the Hodge duality, then the Inner product. But if you define the Inner product first, defining Interior product is irrelevant, and also you can define the Hodge duality based on the Inner product. In the end, we will be able to add a geometrical interpretation to this Inner product, which is really missing to understand what we're actually doing with these calculations.

Inner product

Traditionally the Inner product is defined by pairing between \(\bigwedge\nolimits^k\left(V\right)\) and its Dual space¹¹, \(\bigwedge\nolimits^k\left(V^*\right)\), but I can keep most of the things in \(\bigwedge\nolimits^k\left(V\right)\) space without leaking its dual space, since we're mostly working in an Euclidean space⁶. However, we will try to keep it simple to upgrade the calculations to the more advanced spaces like the Riemannian space¹², where the dual space is a necessity. In fact, you can define the dual space based on the Inner product. This approach is much more beginner friendly in my mind.

Before defining the Inner product let's make some new definitons to make our work easier. Because the vector spaces are linear spaces, we can expand them with their basis. So all k-vectors in a \( n \) dimensional space can be written in \( \mathbf{e}_i \) basis, where \( 1 \leq i \leq n \).

\[ \mathbf{\alpha} = \alpha_{i_1, i_2, \cdots , i_k} \mathbf{e}_{i_1}\wedge \mathbf{e}_{i_2}\wedge \cdots \wedge \mathbf{e}_{i_k} \]

where there are hidden summations on \(i_1, i_2, \cdots , i_k \), as we used Einstein notation¹³. But it has two problems. First, writing \( \mathbf{e}_{i_1}\wedge \mathbf{e}_{i_2}\wedge \cdots \wedge \mathbf{e}_{i_k} \) all the time is hard, so we can replace it with \( \mathbf{e}_{i_1 \cdots i_k} \). Second, there are a lot of duplication because of anti-symmetric property of \( \mathbf{e}_{i_1 \cdots i_k} \), where we can avoid them by sorting the indices. No problem! We can define a sequence, like \( I = i_1, \cdots, i_k \), and use it like \( e_{I} \) to express basis for \(\bigwedge\nolimits^k\left(V\right)\), then we need to define a function by drawing an arrow on top of a sequence of indices to sort them, so \( \overrightarrow{I} \) means sorted \( I \). Thus, we can simplify expanding of a vector like this.

\[ \mathbf{\alpha} = \alpha_{I} \mathbf{e}_{\overrightarrow{I}}. \]

Until here there's nothing new. We also can define the Inner product between two 1-vectors with \( \left\langle ., .\right\rangle \). Therefore, the Inner product between two k-vectors can be defined by the Gram determinant¹⁴ like this

\[ \langle \alpha_1 \wedge \cdots \wedge \alpha_k, \beta_1 \wedge \cdots \wedge \beta_k \rangle = \det \left( \left\langle \alpha_i, \beta_j \right\rangle _{i,j=1}^k\right). \]

Where \( \det \) is the determinant function, and all \( \alpha_i \) and \(\beta_i\) are 1-vectors. Notice both sides of the above Inner product are decomposable k-vectors. Such decomposable k-vectors are called k-blades, where we'll come back to them later, but for now, let's keeping in mind that it's not possible to decompose any k-vector to a k-blade. This is the first restriction of this definition, however, someone can avoid this restriction by just expanding the k-vectors into their basis, where we'll do next. But also it worth to mention that this definition has another restriction too. It is restricted to \( k \) vectors on both sides of the product. We can generalize it, and better than that, we can give it a meaning.

Let's do something new. Let's define the Inner product between a k-vector and a l-vector. To do so, it's easier to work with the basis, therefore, as we expect from linear property of the Inner product to have

\[ \langle \alpha_1 \wedge \cdots \wedge \alpha_k, \beta_1 \wedge \cdots \wedge \beta_l \rangle = \langle \alpha_{1,i_1} \cdots \alpha_{k,i_k}\mathbf{e}_{\overrightarrow{I}}, \beta_{1,j_1} \cdots \beta_{l,j_l}\mathbf{e}_{\overrightarrow{J}} \rangle =\\ \alpha_{1,i_1} \cdots \alpha_{k,i_k}\beta_{1,j_1} \cdots \beta_{l,j_l}\langle \mathbf{e}_{\overrightarrow{I}}, \mathbf{e}_{\overrightarrow{J}} \rangle \]

where \( J = j_1, \cdots, j_l \) is a sequence, similar to \( I \). Before going any further, we need to define a helper function. It's a mini Gram determinant on the \( \langle \mathbf{e}_{i}, \mathbf{e}_{j} \rangle \) based on a set of indecies.

\[ G(I) = \det\left(\left\langle \mathbf{e}_{i_u}, \mathbf{e}_{i_v} \right\rangle _{u,v=1}^{|I|} \right). \]

where \(|I| \) is the cardinality¹⁵ of this set. In other word, it's the number of the distinct elements in the set we can create with the \( I \) sequence. Additionally, we can define that set by \( \{I\} \), so \( |I| = |\{I\}| \). This function, \( G \), can hide all the power of Riemannian geometry¹², and the Dual space¹¹ inside, but it's very simple for the Euclidean space⁶. For all sorted sequences in the Euclidean space \( G(\overrightarrow{I}) = 1 \), but if two of the indices equal, then it's \(0\). Also if non of them are equal then \( G(I) = \sigma(I) \) where \( \sigma(I) \) is the sign¹⁶ of permutation \( \sigma(I) = \sigma(i_1\cdots i_{|I|}) = {(-1)}^{N(I)} \), where \( N(I) \) is the minimum number of permutations you need to sort those numbers.

Now, we just need to define \(\langle \mathbf{e}_{I}, \mathbf{e}_{J} \rangle\). First of all, we need this definition to have a symmetric property, therefore, \(\langle \mathbf{e}_{I}, \mathbf{e}_{J} \rangle = \langle \mathbf{e}_{J}, \mathbf{e}_{I} \rangle \). This let us keep the sequence with smaller number of indices in the second spot, so let's assume \( l \leq k \), or \( |J| \leq |I| \), then we need to define \( P = I - J \) to filter out all the elements in \( J \) from \( I \). We can write the new definition like this

\[ \langle \mathbf{e}_{\overrightarrow{I}}, \mathbf{e}_{\overrightarrow{J}} \rangle = \begin{cases} G(\overrightarrow{P}, \overrightarrow{J})\mathbf{e}_{\overrightarrow{P}} & \text{if } \{J\} \subset \{I\} \\ G(\overrightarrow{I}) & \text{if } \{J\} = \{I\} \\ \;\;\,0 & \text{if } \{J\} \not \subseteq \{I\} \end{cases} \]

This definition looks like a subtraction of indices which is why in the helper Python class that I shared in the end of this post, I named it sub_prod instead of inner_prod. The subtraction concept also could be find in its geometric interpretation, which will be discussed later. Nevertheless, in an expanded version where we don't keep \( |J| \leq |I|\)

\[ \langle \mathbf{e}_{\overrightarrow{I}}, \mathbf{e}_{\overrightarrow{J}} \rangle = \begin{cases} G(\overrightarrow{I - J}, \overrightarrow{J}) \mathbf{e}_{\overrightarrow{I - J}} & \text{if } \{J\} \subset \{I\} \\ G(\overrightarrow{J - I}, \overrightarrow{I}) \mathbf{e}_{\overrightarrow{J - I}} & \text{if } \{I\} \subset \{J\} \\ G(\overrightarrow{I}) & \text{if } \{I\} = \{J\} \\ \;\;\,0 & \text{if } \{I\} \not \subseteq \{J\} \; or \; \{J\} \not \subset \{I\} \end{cases} \]

It looks more complicated than the one we had before, but don't forget that it supports much more than the previous one, and, it's not as complicated as it looks like if I give you some examples in the Euclidean space:

\[ \begin{cases} \langle \mathbf{e}_{2,4,5}, \mathbf{e}_{1,4,5} \rangle &= 0 \\ \langle \mathbf{e}_{2,4,5}, \mathbf{e}_{3,5} \rangle &= 0 \\ \langle \mathbf{e}_{2}, \mathbf{e}_{3,4,5} \rangle &= 0 \\ \langle \mathbf{e}_{2,4,5}, \mathbf{e}_{2,4,5} \rangle &= 1 \\ \langle \mathbf{e}_{2,4,5}, \mathbf{e}_{5} \rangle &= \mathbf{e}_{2,4} \\ \langle \mathbf{e}_{2,4,5}, \mathbf{e}_{4} \rangle &= -\mathbf{e}_{2,5} \\ \langle \mathbf{e}_{2,4,5}, \mathbf{e}_{2,5} \rangle &= - \mathbf{e}_{4} \\ \langle \mathbf{e}_{2,4,5}, \mathbf{e}_{2,4} \rangle &= \mathbf{e}_{5} \\ \end{cases} \]

Looks simple! Notice

Theorem 1: This new definition is also invariance respect to changes over Special orthogonal¹⁷ group in the Euclidean space⁶.

Before going further we need to show that this general definition is compatible with the previous one, which was the case of \( k = l \). From above we have

\[ \langle \alpha_1 \wedge \cdots \wedge \alpha_k, \beta_1 \wedge \cdots \wedge \beta_k \rangle = \alpha_{1,i_1} \cdots \alpha_{k,i_k}\beta_{1,j_1} \cdots \beta_{l,j_k}\langle \mathbf{e}_{\overrightarrow{I}}, \mathbf{e}_{\overrightarrow{J}} \rangle = \\ \alpha_{1,i_1} \cdots \alpha_{k,i_k}\beta_{1,j_1} \cdots \beta_{l,j_k} \det \left( \left\langle \mathbf{e}_{i_u}, \mathbf{e}_{j_v} \right\rangle _{u,v=1}^k \right) = \det \left( \left\langle \alpha_i, \beta_j \right\rangle _{i,j=1}^k\right) \]

Perfect!

Theorem 2: The new definition is compatible with the old one.

Additionally we can define Interior product based on the Inner product like this:

\[ i_\alpha(\beta) := \left\langle \alpha, \beta \right\rangle \]

Thus, we can use the Interior product in terms of the newly defined Inner product, but I can argue that Inner product was our friendly tool since much longer time, so it deserves to be kept and continue to take this responsibility. Hence, we should say bye bye to the Interior product and make it obsolete. Therefore, we'll not use Interior product anymore, at least in this post. Anyway!

The next thing that we can define is the Hodge duality which has an awesome interpretation, where we'll discuss later! But first we need to define the volume form¹⁸. The Volume form has another name in the \( 2D \) Clifford algebra⁴, where we call it imaginary unit, and I like it! Therefore we define it like

\[ i := \mathbf{e}_1\wedge \cdots \wedge\mathbf{e_n} = \mathbf{e}_{1\cdots n}. \]

Which shouldn't be confused by the \(i\) that we used for Interior product. Notice \( n \) is the dimensionality of the space, so all of the 1-vector basis in the space present in the definition of the imaginary unit, \( i \). Before going further let's take a look at below identity.

Theorem 3: Identity \[ \langle i, i \rangle = \langle\mathbf{e}_{1\cdots n},\mathbf{e}_{1\cdots n}\rangle = G(1,\cdots,n) = G_i \] where we defined \( G_i : = G(1,\cdots,n) \).

Alright, the Hodge star operator¹⁰ can be defined like this:

\[ {\star} \alpha := \left\langle i, \alpha \right\rangle. \]

Thus, to get to the old definition we can look at

\[ i = \sigma(\overrightarrow{\bar{I}},\overrightarrow{I}) \mathbf{e}_{\overrightarrow{\bar{I}}}\wedge\mathbf{e}_{\overrightarrow{I}} \]

where \(\bar{I} \) is the the complementary sequence of \(I\) sequence, \(\{\bar{I}\} = \{1,\cdots,n\} \setminus \{I\} \). This makes this happen:

\[ {\star} \mathbf{e}_{\overrightarrow{I}} = \left\langle \sigma(\overrightarrow{\bar{I}},\overrightarrow{I}) \mathbf{e}_{\overrightarrow{\bar{I}}}\wedge\mathbf{e}_{\overrightarrow{I}}\;\;,\;\; \mathbf{e}_{\overrightarrow{I}} \right\rangle = \sigma(\overrightarrow{I},\overrightarrow{\bar{I}}) G_i \mathbf{e}_{\overrightarrow{\bar{I}}} \]

Then you can prove somethig like

Theorem 4: Identity \[ {\star} \left( \alpha \wedge {\star} \beta \right)=\left\langle i, \alpha \wedge \langle i, \beta\rangle\right\rangle = G_i^2 \langle \alpha, \beta \rangle. \] where \( \alpha \) is a k-vector, and \( \beta \) is a l-vector, then in above identity we have \(0 \leq n-(k+(n-l)) \leq n\), which means \( k \leq l \).

Another important property of Hodge star operator is that it makes a duality between \(\alpha\) and \({\star}\alpha\), because:

Theorem 5: Identity \[ {\star}{\star}\alpha = \langle i,\langle i,\alpha\rangle\rangle = G_i^2 \alpha. \] where \( \alpha \) is a k-vector.

Where it can simplify the previous identity like this:

Theorem 6: Identiry \[ \alpha \wedge {\star} \beta= {\star} \langle \alpha, \beta \rangle. \] where \( \alpha \) is a k-vector, and \( \beta \) is a l-vector, then in above identity we have \(0 \leq k+(n-l) \leq n\), which means \( k \leq l \).

Now that we finished with definitions, let's move on to the next level, which is understanding their geometrical meaning.

Geometrical interpretation

First thing that we need to know about k-vectors is that they are not always able to describe geometrical concepts. To clarify, let's explain a concept named k-blade¹⁹. To define it assume we have an explicit point and we're looking to describe a \(1D\) line, \(2D\) surface, \(3D\) volume, etc. The \(3D\) volume is the same as \(3D\) surface, that we mentioned before! The additional information, beside a single point, to describe each of them is called 1-blade, 2-blade, 3-blade, etc. So if you have a point and a 1-blade you have all the information to describe a line. The same for a surface and 2-blade, etc. Notice, a k-blade have to be decomposable to \(k\) 1-vectors, \( \beta_{i} \), so it's always possible to write a k-blade as \( \beta_1\wedge\cdots\wedge\beta_{k} \). The reason we separated k-vectors from k-blades is that generally k-vectors can store more data than k-blade is needed, which means not all k-vectors are describing a k-blade. But how? Let's count the degree of freedom for a k-vector. Because a k-vector is a sum of terms with \( n \) choose \( k \) distinct basis, or

\[ \binom nk = \frac{n!}{k!(n-k)!} \]

then it's their degree of freedom. But when you count the digree of freedom of a k-blade sometimes they are less than that! To count them, let's have a unit k-blade with \( \mathbf{e}_1, \cdots, \mathbf{e}_k \), then we can scale this geometrical object by multiplying it to a number, so we have one scaling degree of freedom. Other degrees can be found by rotating this unit k-blade with a Special orthogonal¹⁷ group, \( SO(n) \), which has \( n \) choose \( 2 \) distinct basis, therefore, a k-blade has

\[ \binom n2 + 1= \frac{n(n-1)}{2} + 1 \]

degree of freedom.

Theorem 7: Let's have a known k-vector, \( \alpha \), and \(k\) unknown 1-vectors, \(\beta_{i}\), then being decomposable means \[ \alpha = \beta_1\wedge\cdots\wedge\beta_{k} \] equation always have an answer, thus, this condition must be satisfied: \[ \frac{n!}{k!(n-k)!} \leq \frac{n(n-1)}{2} + 1. \] which means it's solvable if \[ k \leq 2 \; or \; n - 2 \leq k. \]

I checked the last step with a Python code like this, so it's not a proof up to infinity!

from sympy import factorial
N = 30
for n in range(1, N):
    for k in range(N):
        a = factorial(n)/factorial(k)/factorial(n - k)
        b = n * (n - 1)/2 + 1
        c = a <= b
        d = k <= 2 or n - 2 <= k
        assert c == d

Therefore, the set of k-blades is smaller than k-vectors. Let's call this set \( LL^k(V) \) the set of all k-blades, thus, \(LL^k(V) \subseteq \bigwedge\nolimits^k\left(V\right)\), which means geometric interpretation for all the k-vectors is not possible, at least in the way we used to. This all implies we will restrict ourselves to k-blades instead of k-vectors.

To understand the geometric interpretation of Inner product, let's start with our old friend, the Cross product.

The result of cross product between \( a \), and \( b \) vectors.

But this time we can write the relation between the cross product and the bivector, It's a well-known relationship:

\[ {\star} (\mathbf{A}\wedge \mathbf{B}) = \mathbf{A}\times \mathbf{B} \]

simply because

\[ {\star}\mathbf{e}_{12}=\mathbf{e}_3, \;{\star}\mathbf{e}_{31}=\mathbf{e}_2, \;{\star}\mathbf{e}_{23}=\mathbf{e}_1. \]

But in this picture you can see \( \mathbf{A}\wedge \mathbf{B} \) is perpendicular to \( \mathbf{A}\times \mathbf{B} \), which makes me excited! Does it mean \({\star}\) can make an orthogonal (n-k)-blade out of a k-blade? That looks like a good idea, but before concluding anything let's look at the anti-symmetric property of any k-blade. Assume we have a p-blade, \( \alpha \), and we want to build a m-blade out of it, \( \beta \), where \( p < m \), so we need a q-blade, \( \gamma \), which is totally independent of \( \alpha \), where \( q = m - p \). To do so we just need to use the wedge product like this:

\[ \beta = \alpha \wedge \gamma. \]

It was easy, but it has amazing properties. For instance, if we want to use \(\beta\) and \(\alpha\) again to build up another -blade, read it a blade, you will get zero, \(\alpha \wedge \beta = 0\). This is because those are not any -vector, so you can always write them like \(\alpha=\nu_{1}\wedge\cdots\wedge\nu_{l}\), and \( \beta=\mu_{1}\wedge\cdots\wedge\mu_{m} \), where \(\nu\), and \(\mu\) are 1-vectors, this implies you can use the anti-symmetric property of the wedge product to show \(\alpha \wedge \beta = 0\). Now let's use this property of the Hodge star operator

\[ \alpha \wedge \gamma = \frac{1}{G_i^2} {\star} \langle \alpha, {\star} \gamma \rangle. \]

Which shows in case of

\[ \frac{1}{G_i^2} {\star} \langle \alpha, {\star}\beta\rangle =\alpha\wedge\beta = 0 \]

or

Theorem 8: Identity \[ \langle \alpha, {\star}\left(\alpha\wedge\gamma\right)\rangle = 0 \] where \( \alpha \) is a p-vector, and \(\gamma\) is a q-vector.

Notice, there's no need to mention a condition like \(0\leq p - (n - (p + q)) \leq n \), or \( n \leq 2p + q \leq 2n\), because the cases out of \( [0,n]\) interval, are also giving us zero.

This is wonderful, because if you remember that \({\star}\) could potentially make an orthogonal (n-m)-blade, then this identity gives us another clue, because we expect all orthogonals be perpendicular to any of its componenets. This also give us closer to the meaning of the Inner product, as expected traditionally, if the Inner product is zero then its inputs are perpendicular.

Let's define them and move on. We'll call \(\alpha\), a k-blade, and \(\beta\), a l-blade, are orthogonal, or perpendicular, if and only if \( \langle\alpha,\beta\rangle = 0 \). Therefore, \( {\star} \alpha \) is always perpendicular to \( \alpha \), based on the above identity. That's why it makes duality, because orthogonal of orthogonal should be proportional to the identity operator, \( 1\).

It looks great, we already understood the Hodge star operator, and why it makes dualities, but I'm not satisfied with the understanding of the Inner product. Let's move back a little bit to the Cross product again.

The result of cross product between \( a \), and \( b \) vectors.

Now take a look at the Inner product of \({\star}a \) and \( b \):

\[ \langle {\star}a, b\rangle = {\star} (a\wedge b) = a \times b. \]

But

\[ \langle {\star}a, b\rangle = \langle\langle i,a \rangle, b \rangle. \]

Notice \( i \) is the volume of this \(3D \) space, then \( \langle i,a\rangle \) subtracts \(a \) from the \(3D\) volume, \(i\), to make a perpendicular, then the Inner product between this 2-blade and \(a\) removes its componenet, thus, \(\langle\langle i,a \rangle, b \rangle \) is perpendicular to both \(a\) and \(b\), becuase we removed both of them one by one from the whole volume, \(i\). We had this in a \(3D\) space, but what about a \( n\) dimensional space?

In the case of \(n\) dimensional space, we still have this identity \[ \langle {\star}\alpha, \beta\rangle = {\star} (\alpha\wedge \beta). \] This means if \( \alpha \) is a l-blade, and \(\beta \) is a m-blade, then we can subtract \( \alpha \) from the whole volume, \(i \), then subtract \(\beta\), to get a (n-l-m)-blade that removed both \(\alpha\) and \(\beta\) components from \(i\). Notice \( l + m \leq n \).

Thus, the whole geometrical interpretation of the Inner product for a space with any number of dimensions still is subtraction of one of the inputs from the other one. That's why \({\star}\) gives us an orthogonal in any dimensions.

This is awesome, but I'm not satisfied! What about relations like

\[ \left| a\times b\right| = \left| a \right| \left| b \right| \sin (\theta) \]

or

\[ \left| a . b \right| = \left| a\right| \left| b \right| \cos (\theta) \]

which are valid in \(3D\). What is their correspondence formula for the higher dimensions? To find correspondance formula, first we need to define the norm for -blades. Not too hard! A square of norm of any -vector is

\[ {\left(\left|\alpha\right|\right)}^2 = {\left|\alpha\right|}^2 = \langle \alpha, \alpha \rangle. \]

But for -blades, it has an interpretation. It means the multiplication of all components of a -blade on itself. Now we're ready to look back to the Cross product again! We already found that

\[ |a\times b| = |\langle{\star}a,b\rangle|. \]

However, if the angle between \(a\) and \(b\) is \(\theta\), because the angle between \(a\) and \({\star}a\) is \(\pi/2\), then the angle between \({\star}a\) and \(b\) is \(\pi/2-\theta\). Hence, if we call this angle \(\gamma=\pi/2-\theta\), then \(\sin(\theta)=\cos(\gamma)\), which means we can write

\[ |a\times b| =|\langle{\star}a,b\rangle|=|a||b|\cos(\gamma). \]

You may noticed that \(|{\star}a| = |G_i| |a| \), where \(|G_i|\) is on our way to make sense out of this calculation. On the other hand, the angle between two -blades is useful only in Euclidean space⁶, where \(|G_i| = 1 \), thus, let's stick to these simpler spaces to make progress on the geometrical interpretation.

Theorem 9: In a \(3D\) Euclidean space⁶, we have \[ |\langle{\star}a,b\rangle|=|{\star}a||b|\cos(\gamma). \] where \(a\) and \(b\) are two vectors, and \(\gamma\) is the angle between \({\star}a\) and \(b\).

This shows the Cross product is actually a combination of Inner product with orthogonal of a vector. Hence, it suggests

\[ |\langle \alpha,\beta\rangle|=|\alpha||\beta|\cos(\gamma). \]

Here, we can hide the Trigonometric functions²⁰ in future proofs by using the following

Theorem 10: In any Euclidean space⁶, if we have \[ {|\langle \alpha,\beta \rangle |}^2+{|\langle {\star}\alpha,\beta \rangle |}^2={|\alpha |}^2{|\beta |}^2 \] then \[ |\langle \alpha,\beta\rangle|=|\alpha||\beta|\cos(\gamma) \] where now \(\gamma\) is the angle between \( \alpha \), k-blade, and \( \beta \), l-blade, and \( k + l \leq n \).

First of all you should know that

\[ {|\langle \alpha,\beta \rangle |}^2+{|\langle {\star}\alpha,\beta \rangle |}^2={|\alpha |}^2{|\beta |}^2 \]

is not correct for all \( k \) and \( l \), where \( k + l \leq n \), however, the proof for \(k = 1\) case is straght forward, but before diving into the proof, we need to studdy the symmetries of

\[ A(\alpha,\beta)={|\langle \alpha,\beta \rangle |}^2+{|\langle {\star}\alpha,\beta \rangle |}^2. \]

Theorem 11: \( {|\langle {\star}\alpha,\beta \rangle |}^2 = {|\langle {\star}\beta,\alpha \rangle |}^2 \) for any \(\alpha \) and \(\beta\) -blades.

Hence, \(A(\alpha,\beta)\) is symmetric on substitution of \( \alpha \) and \( \beta \), because of \( {|\langle {\star}\alpha,\beta \rangle |}^2 = {|\langle {\star}\beta,\alpha \rangle |}^2 \), and of course, based on the definition \( {|\langle \alpha,\beta \rangle |}^2 = {|\langle \beta,\alpha \rangle |}^2 \), therefore, we just need to prove it for \( k \leq l \leq n - k \). The other simplification that we can apply on these terms is to rotate the framework in a way that the bigger one, which is the l-blade, simply become one of the basis of the \(LL^k(V)\). Now we're ready to jump to the proof of \( k = 1 \) case. To do so we rotate a unit 1-blade, \( \alpha \), with \(SO(n)\) group, while we keep \( \beta = \mathbf{e}_{i_{1},\cdots,i_{l}} \), \(|\beta| = 1\), a constant by choosing a right framework, then we have

\[ {|\langle \alpha,\beta \rangle |}^2+{|\langle \alpha,{\star}\beta \rangle |}^2 = {|\langle \alpha,\mathbf{e}_{i_{1},\cdots,i_{l}} \rangle |}^2+{|\langle \alpha,\mathbf{e}_{\bar{i}_{1},\cdots,\bar{i}_{n - l}} \rangle |}^2. \]

where as before \(\bar{I} \) is the the complementary sequence of \(I\) sequence, \(\{\bar{I}\} = \{1,\cdots,n\} \setminus \{I\} \). This implies

\[ {|\langle \alpha,\beta \rangle |}^2+{|\langle \alpha,{\star}\beta \rangle |}^2 = \sum_{j\in \{i_{1},\cdots,i_{l}\}} {| \alpha_{j} |}^2 + \sum_{j\in \{\bar{i}_{1},\cdots,\bar{i}_{n-l}\}}{| \alpha_{j} |}^2 = \sum_{j\in \{1,\cdots,n\}} {| \alpha_{j} |}^2 = 1 \]

because of \(|\alpha | = 1\).

Theorem 12: Identity \[ {|\langle \alpha,\beta \rangle |}^2+{|\langle {\star}\alpha,\beta \rangle |}^2={|\alpha |}^2{|\beta |}^2 \] where \( \alpha \) is a 1-blade and \( \beta \) is a l-blade.

The same proof would not hold for all cases because there could be some componenets of \(\alpha\), \( \alpha_{i_1,\cdots,i_{k}} \), that has indices in both \( \{i_{1},\cdots,i_{l}\}\) and \(\{\bar{i}_{1},\cdots,\bar{i}_{n-l}\}\) sets. For instance, take the \( k = 2 \). Notice, it's clear that \( k \leq n - l \), then we have the following.

\[ {|\langle \alpha,\beta \rangle |}^2+{|\langle \alpha,{\star}\beta \rangle |}^2 = \sum_{\{j_{1},j_{2}\}\subset \{i_{1},\cdots,i_{l}\}} {| \alpha_{j_{1},j_{2}} |}^2 + \sum_{\{j_{1},j_{2}\}\subset \{\bar{i}_{1},\cdots,\bar{i}_{n-l}\}}{| \alpha_{j_{1},j_{2}} |}^2. \]

Notice we can write it like this

\[ {|\langle \alpha,\beta \rangle |}^2+{|\langle \alpha,{\star}\beta \rangle |}^2 + \sum_{j_{1}\in \{i_{1},\cdots,i_{l}\}, j_{2}\in \{\bar{i}_{1},\cdots,\bar{i}_{n-l}\}} {| \alpha_{j_{1},j_{2}} |}^2 = 1. \]

But what if we could find a condition that \(A(\alpha,\beta) = 1\) is true, by forcing the extra terms above to be zero. However, it's not always possible to rotate the framework to match one of the -blades, so we need to rewrite this condition in a more general way. To do so, we can define embedded -blades like this. Let's \(\mu\) be a u-blade, and \(\nu\) be a v-blade, where \( u \leq v \), then \(\mu\) is embedded in \(\nu\) if and only if \({|\langle \mu,\nu\rangle|}^{2} = {|\mu|}^{2}{|\nu|}^{2}\).

Theorem 13: Let's have \( \alpha \) a k-blade and \( \beta \) a l-blade, where \( k \neq 1 \;\;and\;\; l \neq 1\). Also let's \(\mu^{u} \) be a u-blade embedded in \(\alpha\), where \( u < k \), and let's \(\nu^{v} \) be a v-blade embedded in \(\beta\), where \( v < l \). Then identity \[ {|\langle \alpha,\beta \rangle |}^2+{|\langle {\star}\alpha,\beta \rangle |}^2={|\alpha |}^2{|\beta |}^2 \] holds if for any \(\mu^{u}\) and \(\nu^{v}\), where \(u + v = k\), we have \( \langle\langle\alpha, \mu^{u}\rangle, \nu^{v}\rangle = 0 \).

Notice, \( \langle\langle\alpha, \mu^{u}\rangle, \nu^{v}\rangle = 0 \) is not the same as \(\langle \alpha,\beta\rangle = 0 \), because the number of equations in them are different. Taking \(k \leq l \leq n-k\) again, in the former, we have

\[ \sum_{i=1}^{k - 1} \frac{l!}{i!(l - i)!}\frac{(n-l)!}{(k-i)!(n - l - k + i)!} \]

equations, but for the later, there are \( \frac{n!}{(l - k)!(n - l + k)!} \) equations.

By the way, this's not a very strange theorem. Someone can have two 2-blades in a \(3D\) space, where we already could measure the angle between them by using their orthogonal 1-blades.

\[ {|\langle {\star}a,{\star}b \rangle |}^2+{|\langle {\star}{\star}a,{\star}b \rangle |}^2= {|\langle a,b \rangle |}^2+{|\langle {\star}a,b \rangle |}^2= {|a |}^2{|b |}^2. \]

Thus, for all \(k=1\), or where we have \(\langle\langle\alpha, \mu^{u}\rangle, \nu^{v}\rangle = 0 \), we proved that

\[ {|\langle \alpha,\beta \rangle |}^2+{|\langle \alpha,{\star}\beta \rangle |}^2 = {|\alpha |}^2{|\beta |}^2 \]

therefore,

\[ |\langle \alpha,\beta\rangle|=|\alpha||\beta|\cos(\gamma) \]

is correct. I'll let you continue on this problem! The good news for you is that I created a playground in Python so you can work on this problem, even that it's so slow for higher \(n\). I have to mention that it's not the most optimized code, or clean code, or structured code, but it's working.

#
# An Euclidean space. Notice there's no type for the `k-vector`s,
# because scalability is not my concern while developing this.
# However, their structure is a list with size 2,
# where it's first element is keeping the basis, and the second
# element is a sympy expression. Also the first element is a list
# of tuples with size 2 themselves. The first spot is the basis
# in the sympy expression, and the second one is the list of
# indices of that basis. Something lik:
#
# [[(`sympy expression for a basis`, `its indices`), ...], `the sympy expression of the k-vector`].
#
# Check `s.volume` for example.
#

from sympy import expand, sin, cos, Abs, simplify, cancel, factorial, symbols, Matrix, zeros, Transpose, init_printing, eye
from functools import reduce
from pathos.pools import ProcessPool
init_printing()

class Space:
    def __init__(self, dimension):
        # dimensionality of the space
        self.N = dimension
        self.basis_name = 'ee_'
        self.basis_map = {}
        self.sym_map = {}
        self.vector_basis = self.get_vector_basis()
        self.volume_base = self.get_volume_base()
        self.volume = self.get_volume()
        self.e = self.get_e()

    def get_basis(self, name):
        if name in self.basis_map:
            return self.basis_map[name]
        self.basis_map[name] = symbols(name, real=True)
        return self.basis_map[name]

    def get_sym(self, name):
        if name in self.sym_map:
            return self.sym_map[name]
        self.sym_map[name] = symbols(name, real=True)
        return self.sym_map[name]

    def sort_basis(self, a, len1, len2):
        #print("a0: ", a)
        alen = len(a)
        sign = 0
        l, r = 0, 0
        while l < len(a) - 1:
            r = l + 1
            while r < len(a):
                if a[l] == a[r]:
                    return (a, 0)
                if a[l] > a[r]:
                    a[l], a[r] = a[r], a[l]
                    sign += 1

                r += 1
            l += 1

        #print("a1: ", a, ", sign:", sign)
        return (a, (1 if sign % 2 == 0 else -1) * self.wedge_coeff(len1, len2))

    def wedge_coeff(self, len1, len2):
        return 1

    def wedge(self, A, B):
        result = 0
        basis = {}
        for e1 in A[0]:
            for e2 in B[0]:
                (sortedBasis, sign) = self.sort_basis(e1[1] + e2[1], len(e1[1]), len(e2[1]))
                # print('e1: ', e1, ', e2: ', e2, ", sortedBasis:", sortedBasis, ", sign:", sign)
                if sign == 0:
                    continue
                e12 = self.get_basis(self.basis_name + reduce(lambda x, y: str(x) + str(y), sortedBasis, ""))
                basis[e12.name] = (e12, sortedBasis)
                result += sign * A[1].coeff(e1[0]) * B[1].coeff(e2[0]) * e12
        scalar_part = Space.scalar_part_wedge_product(A, B)
        if scalar_part[1] != 0:
            for e in scalar_part[0]:
                basis[e[0].name] = e
        return (list(basis.values()), result + scalar_part[1])

    def scalar_part_wedge_product(A, B):
        As = Space.find_scaler_part(A)
        Bs = Space.find_scaler_part(B)
        Av = expand(A[1] - As)
        Bv = expand(B[1] - Bs)
        basis = {}
        if Av != 0:
            for e in A[0]:
                basis[e[0].name] = e
        if Bv != 0:
            for e in B[0]:
                basis[e[0].name] = e
        return (list(basis.values()), expand(As * Bv + Bs * Av + As * Bs))

    def sub_prod(self, A, B):
        result = 0
        basis = {}
        for e1 in A[0]:
            for e2 in B[0]:
                lastCommonIndex = 0
                biggerBasis = e1 if len(e1[1]) >= len(e2[1]) else e2
                smallerBasis = e2 if len(e1[1]) >= len(e2[1]) else e1
                biggerBasisMap = dict((ii, i) for (i, ii) in enumerate(biggerBasis[1]))
                sign = 0
                for index in reversed(smallerBasis[1]):
                    if index in biggerBasisMap:
                        lastCommonIndex += 1
                        sign += len(biggerBasis[1]) - lastCommonIndex - biggerBasisMap[index]
                        del biggerBasisMap[index]
                    else:
                        break

                if lastCommonIndex != len(smallerBasis[1]):
                    continue

                # print("bigger:", biggerBasis[1], ", smaller:", smallerBasis[1],", lastCommonIndex:", lastCommonIndex, ", sign: ", sign)
                if lastCommonIndex == len(biggerBasis[1]):
                    CA = A[1].coeff(e1[0])
                    CB = B[1].coeff(e2[0])
                    result += CA * CB
                    continue

                indices = list(biggerBasisMap.keys())
                indices.sort()
                # print("indices: ", indices)
                e12 = self.get_basis(self.basis_name + reduce(lambda x, y: str(x) + str(y), indices, ""))
                basis[e12.name] = (e12, indices)
                CA = A[1].coeff(e1[0])
                CB = B[1].coeff(e2[0])
                result += (1 if sign % 2 == 0 else -1) * CA * CB * e12
        scalar_part = Space.scalar_part_sub_product(A, B)
        if scalar_part[1] != 0:
            for e in scalar_part[0]:
                basis[e[0].name] = e
        return (list(basis.values()), result + scalar_part[1])

    def scalar_part_sub_product(A, B):
        As = Space.find_scaler_part(A)
        Bs = Space.find_scaler_part(B)
        return (list(), expand(As * Bs))

    def find_scaler_part(A):
        As = A[1]
        for e1 in A[0]:
            if As == 0:
                break
            As -= As.coeff(e1[0]) * e1[0]
        # print("A scalar: ", A[0], ", ", expand(A[1]), " -------- ", expand(As))
        return expand(As)

    def rotation(self, i, j, s):
        result = []
        for row in range(1, self.N + 1):
            r = []
            for col in range(1, self.N + 1):
                if (i == row and i == col) or (j == row and j == col):
                    r.append(cos(s))
                elif i == row and j == col:
                    r. append(sin(s))
                elif i == col and j == row:
                    r.append(-sin(s))
                elif row == col:
                    r.append(1)
                else:
                    r.append(0)
            result.append(r)
        return Matrix(result)

    def unit_vector(self, name):
        return self.unit_multivector(name, 1)

    def transform_vector(self, t, v):
        vm = Matrix([[v[1].coeff(e)] for e in self.e])
        return (
            self.vector_basis,
            (Transpose(t * vm) * Matrix([[self.e[i]] for i in range(self.N)]))[0]
        )

    def unit_multivector(self, name, n):
        t = self.orthogonal_transformation(name)
        v = ([self.vector_basis[0]], self.e[0])
        A = self.transform_vector(t, v)
        for i in range(1, n):
            v = ([self.vector_basis[i]], self.e[i])
            A = self.wedge(A, self.transform_vector(t, v))

        return A

    def orthogonal_transformation(self, name):
        result = eye(self.N)
        for i in range(self.N):
            for j in range(i + 1, self.N):
                result = result * self.rotation(
                    j + 1, i + 1,
                    self.get_sym(name + '_' + str(i + 1) + str(j + 1))
                )
        return result

    def get_volume_base(self):
        return self.get_basis(self.basis_name + reduce(lambda x, y: str(x) + str(y), [i + 1 for i in range(self.N)], ""))

    def get_first_vector_base(self, dimensions):
        l = [i + 1 for i in range(dimensions)]
        v = self.get_basis(self.basis_name + reduce(lambda x, y: str(x) + str(y), l, ""))
        return [[(v, l)], v]

    def get_complementary_of_first_vector_base(self, dimensions):
        l = [i + 1 for i in range(dimensions, self.N)]
        v = self.get_basis(self.basis_name + reduce(lambda x, y: str(x) + str(y),l , ""))
        return [[(v, l)], v]

    def get_volume(self):
        return ([(self.volume_base, [i + 1 for i in range(self.N)])], self.volume_base)

    def vector_syms(self, name):
        return [self.get_sym(name + '_' + str(i + 1)) for i in range(self.N)]

    def get_vector_basis(self):
        return [(self.get_basis(self.basis_name + str(i + 1)), [i + 1]) for i in range(self.N)]

    def get_e(self):
        return [self.get_basis(self.basis_name + str(i + 1)) for i in range(self.N)]

    def vector(self, name):
        a = self.vector_syms(name)
        return (self.vector_basis, reduce(lambda x, y: x + y, [a[i] * self.e[i] for i in range(self.N)]))

    def orthogonal(self, A):
        return self.sub_prod(A, self.volume)

    def norm_square(self, A):
        return self.wedge(A, self.orthogonal(A))[1].coeff(self.volume_base)

    def test_suite(self, difficulty = 2):
        pool = ProcessPool()
        pool.restart(force = False)
        self.test_orthogonal_vector()
        if difficulty >= 4:
            pool.imap(Space.test_orthogonal_transformation, [self])
        self.test_unit_vector()
        if difficulty >= 2:
            pool.imap(Space.test_unit_multivector, [self])
            pool.imap(Space.test_sub_prod_volume, [self])
        if difficulty >= 4:
            pool.imap(Space.test_volume_determinant, [self])
        self.test_sub_prod()
        self.test_norm_square()
        self.test_sub_prod_commute()
        self.test_sub_prod_double_orthogonal()
        self.test_identity(difficulty)
        pool.close()
        pool.join()

    def test_orthogonal_vector(self):
        print("test_orthogonal_vector")
        A = self.vector('a')
        for i in range(1, self.N):
            B = self.vector(chr(97 + i))
            A = self.wedge(A, B)
            orthogonalA = self.orthogonal(self.wedge(A, B))
            assert expand(self.sub_prod(orthogonalA, A)[1]) == 0

    def test_orthogonal_transformation(self):
        print("test_orthogonal_transformation")
        t = self.orthogonal_transformation('a')
        assert simplify(Transpose(t) * t) == eye(self.N)

    def test_unit_vector(self):
        print("test_unit_vector")
        A = self.unit_vector('a')
        # print("AA:", simplify(self.sub_prod(A, A)[1]))
        assert simplify(self.sub_prod(A, A)[1]) == 1

    def test_unit_multivector(self):
        for i in range(1, self.N):
            print("test_unit_multivector for :", i)
            A = self.unit_multivector('a', i + 1)
            # print("i:", i, "|A|: ", simplify(self.sub_prod(A, A)[1]))
            assert simplify(self.sub_prod(A, A)[1]) == 1

    def test_sub_prod_volume(self):
        print("test_sub_prod_volume")
        A = self.vector('a')
        for i in range(1, self.N):
            B = self.vector(chr(97 + i))
            A = self.wedge(A, B)
        C = self.sub_prod(A, A)
        aElement = expand(A[1]).coeff(self.volume_base)
        # print("aElement * aElement: ", expand(aElement * aElement))
        # print("C: ", expand(C[1]))
        assert expand(C[1] - aElement * aElement) == 0

    def test_volume_determinant(self):
        print("test_volume_determinant")
        A = self.vector('a')
        m = []
        m.append([A[1].coeff(A[0][i][0]) for i in range(self.N)])
        for i in range(1, self.N):
            B = self.vector(chr(97 + i))
            m.append([B[1].coeff(B[0][i][0]) for i in range(self.N)])
            A = self.wedge(A, B)
        m = Matrix(m).det()
        aElement =  expand(A[1]).coeff(self.volume_base)
        # print("m: ", m)
        # print("aElement: ", aElement)
        assert expand(m - aElement) == 0

    def test_sub_prod(self):
        print("test_sub_prod")
        a = self.vector_syms('a')
        b = self.vector_syms('b')
        A = self.vector('a')
        B = self.vector('b')
        P = self.sub_prod(A, B)
        # print("P: ", P)
        assert P[0] == []
        assert expand(P[1] - reduce(lambda x, y: x + y, [a[i] * b[i] for i in range(self.N)], 0)) == 0

    def test_norm_square(self):
        print("test_norm_square")
        a = self.vector_syms('a')
        A = self.vector('a')
        B = <F25>self.norm_square(A)
        norm = reduce(lambda x, y: x + y, [a[i] * a[i] for i in range(self.N)], 0)
        # print("norm: ", norm)
        # print("B: ", B)
        assert expand(B * B - norm * norm) == 0

    def test_sub_prod_commute(self):
        print("test_sub_prod_commute")
        A = self.unit_vector('a')
        B = self.unit_vector('b')
        assert expand(self.sub_prod(A, B)[1] - self.sub_prod(B, A)[1]) == 0

    def test_sub_prod_double_orthogonal(self):
        print("test_sub_prod_double_orthogonal")
        A = self.vector('a')
        B = self.orthogonal(self.orthogonal(A))[1]
        assert expand(A[1] * A[1] - B * B) == 0

    def test_identity(self, difficulty):
        for l in range(1, self.N):
            self.test_identity_with_dimensions(1, l)
        if difficulty >= 3:
            pool = ProcessPool()
            pool.restart(force = False)
            for k in range(2, self.N):
                for l in range(k, self.N - k + 1):
                    pool.imap(Space.test_identity_with_dimensions, [self], [k], [l])

            pool.close()
            pool.join()

    def test_identity_with_dimensions(self, k, l):
        print("test_identity_with_dimensions for :", k,", ", l)
        A = self.unit_multivector('a', k)
        B = self.get_first_vector_base(l)
        E = self.sub_prod(A, self.orthogonal(B))
        F = self.sub_prod(A, B)
        G = self.sub_prod(E, E)
        H = self.sub_prod(F, F)
        P = expand(G[1] + H[1])
        R = simplify(P)
        if R == 1:
            print("identity works for n: ", self.N, ", k: ", k, ", l: ", l)

where you can run the tests like the following.

s = Space(4)
s.test_suite(4)

---

References

Cite

If you found this work useful, please consider citing:

@misc{hadilq2023InnerProduct,
    author = {{Hadi Lashkari Ghouchani}},
    note = {Published electronically at \url{https://hadilq.com/posts/inner-product/}},
    gitlab = {Gitlab source at \href{https://gitlab.com/hadilq/hadilq.gitlab.io/-/blob/main/content/posts/2023-03-05-inner-product/index.md}},
    title = {The Inner product},
    year={2023},
}