Since my master thesis¹, "Holographic Superconductors and Rotating Black Hole", I'm getting thriled by superconductors. It's not the case for everything that I worked on! For instance, I'm not a fan of Ads/CFT that I worked on it back then. Nonetheless, superconductors are so fascinating. High-temperature superconductors² could change our life in a way that we'll call it superconductor age, if we wouldn't get extinct by then, the same way that we had stone age, iron age, and we're living in the silicone age. Writing of superconductor age, a piece of puzzle that I'll write here about is a speculation that a version of superconductor age has already passed!

---

Above wallpaper reference¹

After my thesis I didn't stop and wrote "Conservation of Optical Chirality in Superconductors as a measure of 5 dimensional Elecromagnetism"². This paper shows that London equations³ can be derived from 5 dimensional Electromagnetic equations, without any further assumptions or arguments, which is an advantage if you are okey to have extra dimension in your theory. The London equations, which we'll refer them as electromagnetic equations, are experimentally tested, but they first emerged to explain the Meissner effect⁴. The Meissner effect⁴ is happening in Type I⁵ and Type II⁶ superconductors. To understand the differences between them you just need to look at this picture from Wikipedia, and its subscribtion.

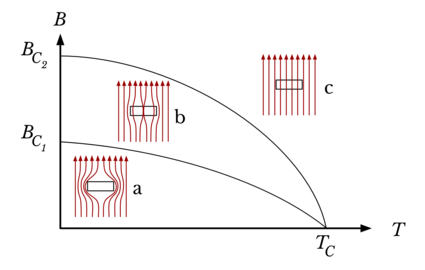
Superconductive behavior under varying magnetic field and temperature. The graph shows magnetic flux B as a function of absolute temperature T. Critical magnetic flux densities \( B_{C_{1}} \) and \( B_{C_{2}} \) and the critical temperature \( T_{C} \) are labeled. In the lower region of this graph, both Type-I and Type-II superconductors display the Meissner effect (a). A mixed state (b), in which some field lines are captured in magnetic field vortices, occurs only in Type-II superconductors within a limited region of the graph. Beyond this region, the superconductive property breaks down, and the material behaves as a normal conductor (c).

So far so good. But the question that everyone jump on it after hearing the 5th dimension is that where is it? Why we cannot move along it? These are valid questions that needs to be addressed. Also this is not the first theory that proposed extra dimension and people asked such questions. For instance, in the Kaluza theory⁷ the fifth dimension is generating the electromagnetic equations themselves. However, the Kaluza–Klein theory justified those questions by assuming that the extra dimension is compact⁸, which will lead to some wrong predictions. Here we'll discuss another method to answer those questions.

Notice with Kluza theory⁷ the electomagnetic equations emerge from Einstein field equations⁹, so if we could explain the existance of the extra dimensions, Not just electromagnetism, but it also can be a framework to talk about Yang–Mills theory¹⁰, which is the basis of Quantum field theory, and the Standard Model¹¹ then we somehow could reach to a quantum gravity theory. Below I'll explain where is that extra dimension, but without applying it to the Kluza theory, even that it looks like everything is done before¹². In fact, String theorists¹³ built a good ground for this approach. Their only mistake is that strings are not observable and compact dimensions is not a satisfying assumption. Someone can use below approach to address those issues, but it's not what we'll do here.

Extra dimensions

Let's have a superconductor again! Clearly the fifth dimension, that is responsible for supercondictivity state, is not a dimension like other spacial dimensions, that a particle could walk a long distance on it. Here, we want to explore the possibility of having such an extra dimension by providing a model to how it looks like. I have to mention that I had this idea for a decade. I should have draw some picures in my paper² to explain it, but I thought the readers are responsible to make sense out of my writing. Apparenlty I was wrong! So I'm trying to explain it easily, in the way that I understood it. Therefore, let's jump on it. Take a look at this picture.

It's a fact that current mathematical tools cannot model the surface of water bubbles in this picture as a manifold¹⁴. By the way, that's why we don't have a quantum gravity theory! Any advancement in human life is depending on building tools, we didn't have the right tools to build such a theory. The reason is all of our theories are built on top of manifolds¹⁴, where it couldn't explain this simple surface/space around our every day life. Let's simplify this picure then explain why. Let's zoom more!

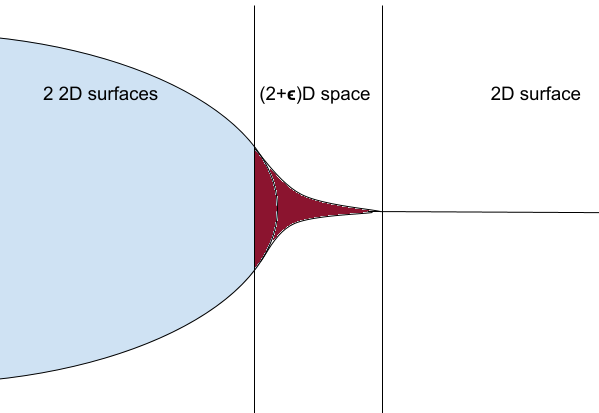
As we argued this is not a manifold, so let's call it manimuchfold! I would call it hyper-manifold, but the name is already taken, so let's have fun with this name. A manimauchfold is a space that can be covered by patches with different dimensionallity. Notice, as the same as what we have for manifolds, those patches must be able to overlap each others on their boundaries. For instance, in above picture of an abstract bubble on the surface of water, you can see we have a 2 dimensional surface on the right, which is the surface of the water, then a surface with \( 2+\epsilon \) dimensions in the middle, with purple color, and two other two dimensional surfaces on the left side of the picture, which are the surfaces of the bubble inside and outside of the water. Be aware that the middle patch is not a 3D space, because a particle cannot move long distances on the \( z \) axis, where the \( z \) axis is prependicular to the surface of the water on the right.

The claim is that the same model can be used to describe superconductors. Inside of a Type I superconductors are two smoothly curved \( (3+1)D \) spaces that are bent into a fourth spacial dimension, where its abstract model would exactly be like the one we draw for a bubble above. Notice for a superconductor, you have to maintain the dimensionallity of the patches, for instance, the right side would be a \( (3+1)D \) patch, the middle one is a \( ((3+\epsilon)+1)D \) patch, and the left side would be two \( (3+1)D \) patches. We're still running by imagination, so based on my intuituon, when I think about how come the type II superconducttivity could have the magnetic field vortices, its model must be something like this

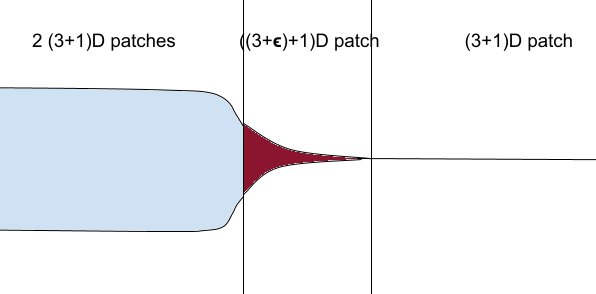
Its difference is that the curvature of the bent matter into the extra dimension is changing much more than what we had for type I superconductivity.

Be aware that, in the \( (3+\epsilon)+1 \) dimensions space in the middle, locally we can think of any field equations as a \( (4+1)D \) equations, therefore, as long as the \( (4+1)D \) electromagnetic equations includes the London equations, this manimauch fold will produce the Meissner effect⁴. Thus we proved such a manimuchfold space would have reproduce at least one of superconductor's behaviour. The other important behaviour of superconductors is that they have zero resistance¹⁵, which based on the above digrams in the middle of two \( (3+1)D \) patches inside the superconductor we have an empty space, the blue color region in the diagrams above, which implies a very long mean free path¹⁶, that increases the electrical mobility¹⁷, which leads to decreasing the electrical resistivity¹⁵, therefore, we'll get a resistance that's very close to zero. So we proved that such a manimuchfold would get us a superconductor with all its behaviour. The only thing we need to do is to describe our model precisely in a mathematical way.

I have to mention that regarding the extra dimensions in the Kluza theory⁷, this model needs another ingeridiant to work, that I'm not going to write about it in this post, but the general idea is close.

Bubble

It's so simple and so fascinating. I have to mention that we already know a bubble that's floating in the air can be described by manifolds. Actually we have more than that. We can write the equations of motion of the bubble in the air, which is basically equations for minimizing the Curvature of its Riemannian manifold¹⁸, then we can find the bubble's \( 2D \) sphere as their solution. Bubbles are interesting because their equations of motion are exactly the same as what we have in General Relativity¹⁹ for the space-time, except the time signature in the metric and the number of dimensions, but the rest is exactly the same. This is why we have to study bubbles to understand the space-time. Additionally, we can do the same for the surface of the water, then find the flat \( 2D \) surface as the solution of those equations. Thus, in the above diagram of a bubble, the equations for the \( 2D \) surface in the right side and the equations for the two \( 2D \) surfaces on the left side are the same, therefore, we can solve those equations and find the solutions. The only patch that we don't know its equations, therefore its solutions, is the middle patch, the \((2+\epsilon)D \) surface.

Notice, the right side of the \((2+\epsilon)D \) patch must be a \( 2D \) flat surface to overlap with the patch outside of the bubble. Also on the left side of the \((2+\epsilon)D \) patch there must be overlaps with the two \(2D \) surfaces on the buble, thus, the dimensionality of \((2+\epsilon)D \) patch is changing over its coordinates, and what we mentioned as \((2+\epsilon)D \) is just the maximum dimensionality of that patch. This is what's making it hard to describe precisely, in the same way as what we can do for the left and the right side in the above diagram.

Here is our plan. We start by explaining how to derive equations of motions from minimizing the curvature. Then we try to remove a dimension from the equations and observe what's happening if we have multi dimensional patch on a manimuchfold. Then we'll try to fix the math and build everything upon that fix.

The Einstein–Hilbert action²⁰ is the optimization of Curvature of its Riemannian manifold¹⁸ that we need to find the equations of motions for both bubble and space-time. It looks like this.

\[ S = \int R \sqrt{-g} \mathrm{d}^4x \]

Notice we used units that make our calculation easier, so its coefficient is \(1\). Also you should know that by optimizing the curvature we just mean we demand \( \delta S = 0 \). This is how a Physics theory derive its equations of motions, but we'll not going to find them in this post anyway. We're just looking to be able to write this condition in a mathematical way for our mysterious patch on the manimuchfold. Based on our plan, we're going to make sense out of the curvature of a patch with multiple dimensions. But let's first expand this definition and see what we have. The curvature¹⁸ \( R \) is

\[ R(u,v)w=\nabla_{u}\nabla_{v} w - \nabla_{v} \nabla_{u} w -\nabla_{[u,v]} w \]

where \( u \), \( v \), and \( w \) are some vectors. Also \( [.,.] \) is the Lie bracket²¹, which we don't need it if we choose coordinate vectors, \( u = \partial/\partial x^{i} \) and \( v = \partial/\partial x^{j} \), because in this case \( [u,v]=0 \). The Covariant derivative²², \( \nabla \), is

\[ \nabla_{\mathbf{e}_{j}} u = \nabla_j u = \left( \frac{\partial u^i}{\partial x^j} + u^k {\Gamma^i}_{kj} \right) \mathbf{e}_i \]

where typically the basis are \( \mathbf{e}_i = \partial/\partial x^{i} \), and the Christoffel symbols²³ are

\[ {\Gamma^i}_{kl} = \frac{1}{2} g^{im} \left(\frac{\partial g_{mk}}{\partial x^l} + \frac{\partial g_{ml}}{\partial x^k} - \frac{\partial g_{kl}}{\partial x^m} \right) \]

and finally, \( g_{ij} \) is the Metric tensor²⁴, and \( g = \det g_{ik} \) is the determinant of the metric tensor, also \( g^{im} \) is the inverse matrix²⁵ of \( g_{im} \), which means they satisfy \( g^{im}g_{mj} = \delta^{i}_{j} \). You should probably know about these stuff before to make sense out of this writting, but I mentioned them to add references if you are started and want to dig more.

Now that we know what it means to optimize the curvature, we need to understand what it means to remove a dimension from a manimuchfold. Removing a dimension means no particle will try to move on that direction. As you may know particles are moving on geodesics, so we need to take look at geodesic equation of motion²⁶. They are like this

\[ {d^2 x^i \over ds^2}+{\Gamma^i}_{jk}{d x^j \over ds}{d x^k \over ds}=0 \]

where \( s \) is a scalar parameter of motion. Let's assume we want to remove dimensoin \( n \). If a particle is already moving in a sub-space, that is defined by removing \( n \), something like the water surface where \(n \) would be the \( z \) direction, \( d x^k / ds \) will be tangent²⁷ to that sub-space all the time, therefore, to eleminate that particle to moving out of the sub-space on the dimension \( n \) we need to set \( {d^2 x^n / ds^2} = 0 \). But in the case of a bubble it's not actually zero. It's so close to zero, because there are still a lot of geodesics cut the bubble's surface, for instance we can see inside the bubble because light's geodesics are cutting the bubble's surface, but this argument is enough for us to know how we can remove a coordinate, \( n \), from the manimuchfold. Thus, a condition like \( {d^2 x^n / ds^2} \rightarrow 0 \) will satisfy all we really want. This implies

\[ {\Gamma^n}_{jk}{d x^j \over ds}{d x^k \over ds} = \frac{1}{2} g^{nm} \left(\frac{\partial g_{mj}}{\partial x^k} + \frac{\partial g_{mk}}{\partial x^j} - \frac{\partial g_{jk}}{\partial x^m} \right){d x^j \over ds}{d x^k \over ds} \rightarrow 0 \]

But this equation should hold for all different paths, so for all \( d x^k / ds \) inside our sub-space, that is defined by a coordinate, \( n \), thus, \( g^{nm} \rightarrow 0 \) must hold for all \( m \), including \( m = n \). Here we reached to the core problem of our understanding of how manimuchfold could possibly have different dimensionality in different points, because all elements in a row of the inverse matrix are zero, \( g^{nm} \rightarrow 0 \), therefore, its determinant would be zero, \( \det(g^{ij}) \rightarrow 0 \). This fact dictates that we cannot construct \( g_{ij} \) from \(g^{ij} \), thus, we cannot calculate curvature and optimize it to get to our target with ordinary methods.

In this point, I have to apologize for not continuing on my method to follow what I've promised above. I decided to write about my method in the future, but to avoid further explanation of changes on my plan to solve it, I just removed a little bit from this post to be added in the future one along the complete explanation. At least I explained how to remove a dimension in a patch of manimuchfold! Hope you are not disappointed. There are still a lot of good points and ideas in this post.

Mindset shift

Everyone is talking about 4 fources that should be united in a quantum gravity theory, then they continue, but gravity is not a force! Then they full stop! Hey! I'm waiting for the resolution! Nevermind! Maybe we could all agree on my cooked up resolution here.

It looks like we only have two choices, either we should accept all of them are forces, or maybe we should consider the possibility that non of them is a force. If non of them is a force, how we should undertand the phenomenas that we understood by using forces. As someone who did this practice before, I advise to start with Surface tension²⁸. Yes! Something like water's surface tension, the same as the one that created our bubble above. This is how Wikipedia described it.

Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) to float on a water surface without becoming even partly submerged.

also

There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract. Second is a tangential force parallel to the surface of the liquid. This tangential force is generally referred to as the surface tension.

In the following diagram the red arrows supposed to explain how cohesive force in surface tension of a liquid is working.

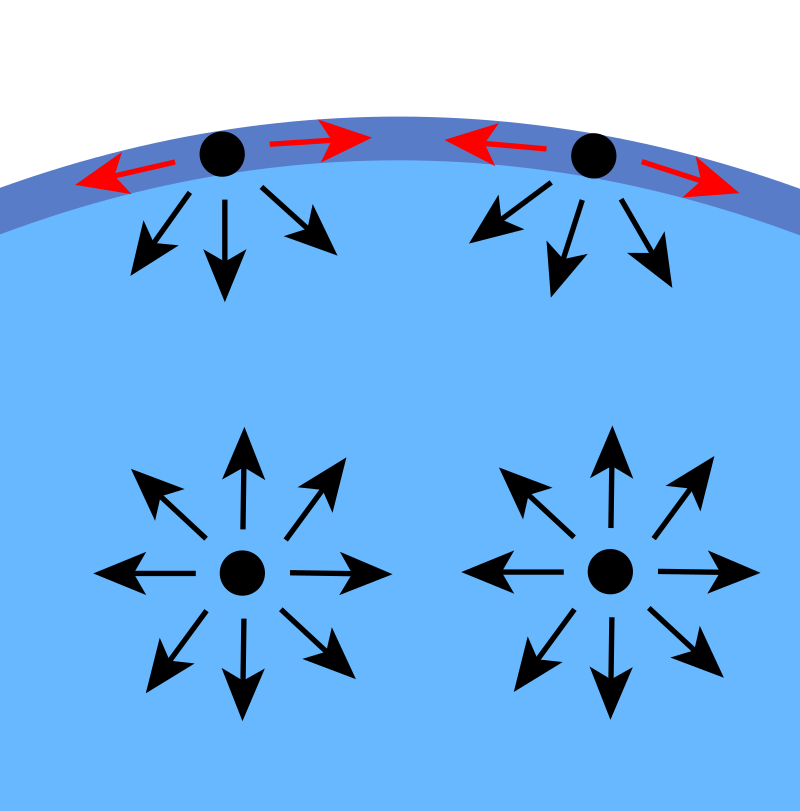
Nonetheless, the current accepted claim is that the surface tension is caused by molecular attraction among molecules inside the water, which is an electromagnetic force. So the current explanation for surface tension needs electromagnetic force. But I don't know about you, for me, this argument is not convincing! How come the red arrows in the above diagram are bigger forces than the ones inside the liquid? They must be bigger, because the surface can hold more weight, such as razor blades, but when only if a corner of the same razor blade get inside the liquid, the razor would sink, so where are the bigger forces to keep it on the surface in this situation?! Now that I invoked your doubt about current explanation, let's have a more convincing explanation.

Assume null-geodesics pass from a point on a surface of a liguid as shown in below diagram, similar water's surface as the one above. For general cases of all geodesics, non-null geodesics, they follow the same dot-lines, with different velocities, so the diagram will stay the same.

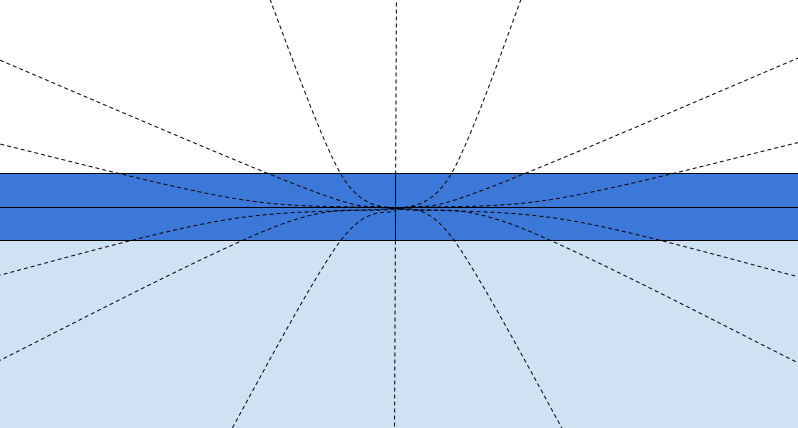
as you can see for each point on the surface that could be common with a point on the rasor, if the geodesics are parallel to the rasor blade's surface, then they will stay on the surface, but if a corner of the razor blade gets into the liguid, it have to follow the geodesics, therefore, it'll sink. How simple and convincing is this?

The surface tension is defined for the boundary between a liquid and air, but above argument can be extended to any other surfaces and boundaries. In the general sense, I defined before a structure as "A structure is a pattern in the single tensor field with rigid enough boundaries that let it have one or multiple resonance frequencs on any kind of wave(field)" in the Reproducibility²⁹ post, so based on above argument we can generalize all the boundaries of all structures to apply metrics and geodesics on all of them.

Be aware that here we applied the same assumpsion as what we did in Understanding Quantum Mechanics³⁰.

Gravity in General Relativity has two parts. The first part is the Equivalence Principle which will lead us to Riemannian geometry, and the second part is the Einstein field equations. Here we will ignore the second part, but will accept the space-time can have curvature even in short distances without need of any huge mass, which is the first part.

Therefore, we don't need mass to explain these kind of space-time curvature. All boundaries have this kind of space-time curvature, without support of any mass that satisfies Einstein field equations⁹.

Thus, this curvature is happening on the surface of solids too, but the geodesics in above diagram are staying for much more distances parallel to the surface of the solid, therefore, for instance, most geodesics of the particles of your hand that pushes the wall end up just moving parallel to the surface. Again, how simple is this explanation? If you get deep inside the Newton's laws of motion³¹, you could see all the forces are applied on the surfaces, except the gravity that's already explained by metric fields and geodesics in the General Relativity before, which means we can explain all behaviour of matter that were explained by those three laws, just by study of the surface's curvatures.

But this is not the only argument we have! We can provide more evidences for surfaces' curvature. Let's take a look at another mystery that everyone ignores! Why does light slow down in water?

This video provided two wrong explanation of why light slows down, and a supposedly right explanation in the end. He rejects the two first because the scattering light from reflection and emision would not explain the one direction that light keeps in the water. However, in the third explanation we still have the same problem, becouse what he called as the second wave should have the comparable amplitude of the original wave, but an electron will emit light in all directions, so again the single direction of light is violated by the supposedly the correct explanation. With all respect to Dr. Don Lincoln, who I learned a lot from him, this is how the corrent science's society works, we refuse to say we don't know sometimes!

Anyway, let's look at the metric, geodesics, and curvature explanation of the boundaries, then try to explain the speed of light problem. But before that let's go back in time and review how we came to the conclusion that space-time is curved in the first place. In General Relativity, we assumed light always travels on the geodesics, so if the geodesics, which are the shortest path from the origin to the destination of the light, are curved, then the space-time is curved. But it's harder to apply this argument on small scale objects, like water and air surface, because in General Relativity the test object, that we want to measure its path, is very small respect to the wavelength of the metric field. For instance, in Schwarzschild metric³², the wavelength of the metric field is infinite, therefore any particle, like Earth is comparably smaller than the field's wavelength, thus Earth will move on the geodesics of that metric field. But in the case of water and visible light, the wavelength of the light is comparable to the depth of the surface between water and air. This imples we need to improve our techniques to find the geodesics in such a case. In fact, in experiments with Dispersive prism³³, we observe that light with different frequencies would take different paths, so different geodesics.

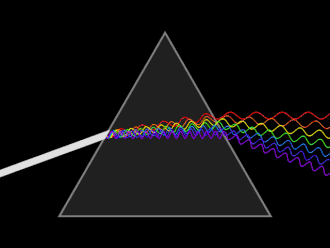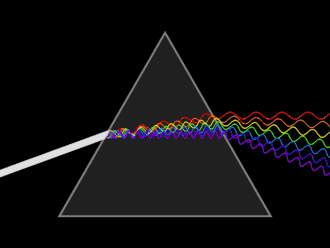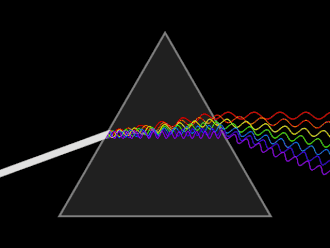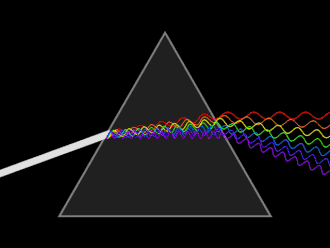
This behaviour is different from what Equivalence principle³⁴ suggests if you forget to take the above condition into account. This implies Equivalence principle is applicable only if the test object is very small comare to the wavelength of the metric field. In other words, if the wavelength of the test object is comparable to the wavelength of the metric field, each wavelength would take their own geodesics. This notion will pave the way for the Klein theory because as you may know particles with different charges would take different geodesics.

Let's dig in! The null-geodesics are a gift to simplify our calculation. On a null geodesic, with \( x^i=\gamma^i(\tau) \), and \( \tau \) as its parameter, we have

\[ g(\dot\gamma(\tau),\dot\gamma(\tau)) =g_{ij} \dot\gamma^{i}(\tau) \dot\gamma^{j}(\tau) = 0 \]

where \( \dot\gamma^{i}(\tau)= d \gamma^{i}(\tau) / d\tau \). Notice \( g_{ij} \) itself is a function of space-time, where we calculate it on the null-geodesic's path, so by writing it in the full details we have

\[ g_{ij}(\gamma(\tau),\gamma(\tau)) \dot\gamma^{i}(\tau) \dot\gamma^{j}(\tau) = 0 \]

Be aware that \( \gamma(\tau) \) is independent of \( \dot\gamma(\tau) \) in the same way that they are independent in the Euler–Lagrange equation³⁵ calculation, because the space-time is independent from its tangent bundle. Soon we'll use this fact. Anyway, this single geodesic line doesn't have enough information, that we need for a monochromatic radiation. Information like its frequency. To add those information to the model we need a group of geodesics, which we can gather them together with a new parameter \( \lambda = \int ds \), where \( ds=\sqrt{-g_{\mu\nu}(x) dx^\mu dx^\nu} \) is a timelike line element³⁶. Notice, \( d/d\lambda \) vector is not parallel to geodesics' lines. To simplify your imagination, you can think of \( \lambda \) as the worldline of an observer, who is in the path of all geodesics of that radiation, so he/she can measure its frequency by oscillating with the same frequency of that radiation. Therefore we have

\[ g_{ij}(\gamma(\tau, \lambda),\gamma(\tau, \lambda)) \dot\gamma^{i}(\tau, \lambda) \dot\gamma^{j}(\tau, \lambda) = 0 \]

where we can calculate its Fourier transform³⁷ like this

\[ \int_{-\infty}^{\infty} g_{ij}(\gamma(\tau, \lambda),\gamma(\tau, \lambda)) \dot\gamma^{i}(\tau, \lambda) \dot\gamma^{j}(\tau, \lambda) e^{-i \omega \lambda} d\lambda = 0. \]

The \( \omega \) would be an angular frequency of the observer, which we can conclude it's the radiation's angular frequency. Notice even after adding \( \lambda \) to the parameters, \( \gamma(\tau,\lambda) \) are independent of \( \dot\gamma(\tau,\lambda) \), therefore, let's give it a new name to make it clear, \( u^i = \dot\gamma(\tau,\lambda) \) is a vector parallel to geodesics that is passing from any point in the cureved space-time of the boundary. Thus we get

\[ \widetilde{g}_{ij}(\tau,\omega) = \widetilde{g}_{ij}(\gamma(\tau,\omega),\gamma(\tau,\omega)) = \int_{-\infty}^{\infty} g_{ij}(\gamma(\tau, \lambda),\gamma(\tau, \lambda)) e^{-i \omega \lambda} d\lambda \]

where \( \widetilde{g}_{ij}(\tau,\omega) \) is the fourier transformation of \(g_{ij}(\gamma(\tau, \lambda),\gamma(\tau, \lambda))\), therfore

\[ \widetilde{g}_{ij}(\tau,\omega)u^{i}u^{j} = 0. \]

Notice this equation itself dictates that \( \widetilde{g}_{ij} \) is not a function of \( \tau \) anymore, because \( u^{i} \) keeps the path on the geodesic.

\[ \widetilde{g}_{ij}(\omega)u^{i}u^{j} = 0. \]

This is useful because we can compare it with Refractive index³⁸ equation. So generally we accept the above equation for the boundary of any two mediums, but for simple mediums we can simplify it to get to the simple case of refractive index. For instance, let's have a constant time coefficient for metric, \( \widetilde{g}_{00} = c^2 \), where \( c \) is the speed of light in vacuum. Notice, this assumption is consistent with the usual assumption of constant angular frequency of radiation of electromagnetic waves on both sides of the boundary, which is used in a lot of textbooks to prove the Snell's law³⁹. Also let's assume the metric is diagonal on \(x, y , z \) coordinates, where \( x-y \) is the surface of the boundary, and \( z \) is orthogonal to the boundary. Therefore, the radiation's velocity in the boundary is

\[ v = \frac{dz}{dt} = \sqrt{\widetilde{g}_{00} \over \widetilde{g}_{zz} } = \frac{c}{\sqrt{\widetilde{g}_{zz}}} = \frac{c}{n} \]

which implies

\[ n = \sqrt{\widetilde{g}_{zz}(\omega)} \]

The fact that we can derive how light slows down in the medium, and we're one step away to prove the Snell's law from our model, shows we're close to a correct model for the boundaries between mediums.

Having this evidences, we can think of an experiment in our mind. If the boundaries of mediums are actually curved space-time then light must be bent close to those areas. But wait! This experiment is already conducted millions of times, and we call it Diffraction from slits⁴⁰.

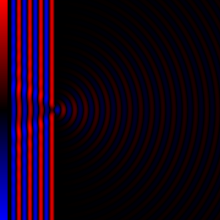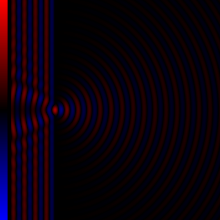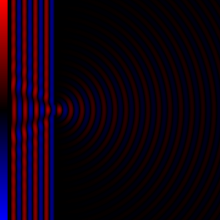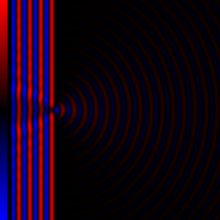
As you can see in above image, the wave is not moving only on the \( x \) direction after passing the slit. The wave starts moving on slops which is considered as obvoius as far as I know, but why? Our above understanding of the boundaries suggests that geodesics that wave is moving on them are actually bent on the boundarie of the slit itself, therefore, wave could propagate on a direction that has a \( y \) element too.

Dark matter is not a matter

Making a relation between bending the waves close to boundaries and bending of light close to the dark matter halo is an eureka moment, something like a falling apple for Newton, so you can consider it as a consequence of the mind shift we experienced above.

By this model we can consistently think of the curvature of space-time everywhere, instead of thinking by forces. This consistency allows us to think about more general cases. We can think of all boundaries as a step function in the space-time metric fields, something like

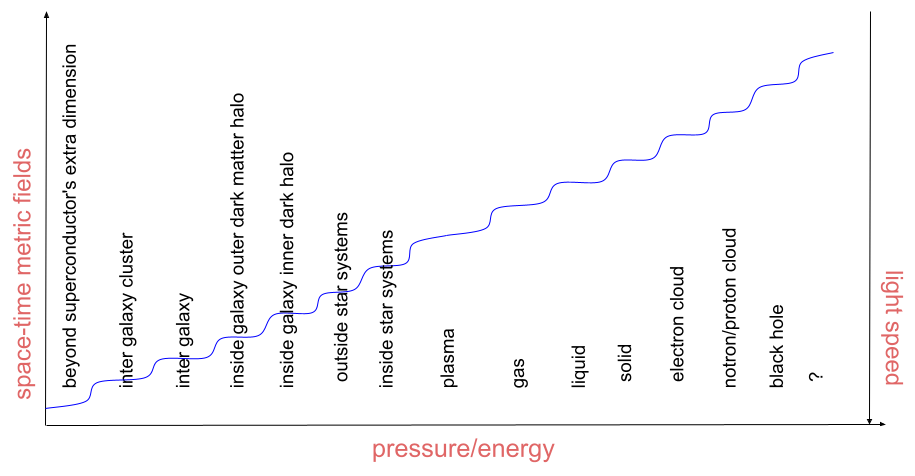
Which we call it energy ladder diagram. The only fact in this diagram is the behaviour of the space-time metric field that jumps from one place to another place, like a step, in a way that it builds up all boundaries among objects in our reality. The rest of the information in this diagram are just added to fly your imagination, and to show how this concept could be vast.

Anyway, this diagram displays how increasing the energy, which is easier to think of it as pressure in this case, increases the value of mertic fields, where in a lot of cases could mean decreasing of the speed of light in those mediums. The idea here is that each medium has its own, almost constant, metric, which you can calculate the speed of light in that medium based on that metric. Notice, this metric doesn't need a mass to support its existance, like what Einstein's field equations suggests. For instance, this implies we don't need acual dark matter to justify existance of the inner/outer dark matter halo⁴¹.

Also we intentionally didn't explicitly mention which element of the metric field in this diagram is shown, because the existance of the steps are the main point, where the boundaries exist.

Be aware that what we call inner/outer dark matter halo here is observable, but dark matter is not observed and this model adds more doubts about its existance, however, that region of space is named wrongly based on the dark matter, so we have to stick to that name, even that there's no reference to the dark matter itself here. In fact, it's easier than ever to reject the dark matter idea, because there are two evidences for it. We already rejected one evidence to be the case, which is the bending of light over the dark matter halo's boundary. The second one, is the speed of stars around the galaxies, which needs a little bit of explanation to resolve this so called big problem away.

The speed of stars around some galaxies could be calculated with Modified Newtonian dynamics⁴², or Milgrom's law, with in the region far away from the center of the galaxy, which they call it deep-MOND regime, \( a \ll a_{0} \), the Newton's law of universal gravitation⁴³ would change its formula to

\[ \frac{GMm}{r^2}=m\frac{{\left(\frac{v^2}{r}\right)}^2}{a_{0}} \]

or in a less encrypted way

\[ ma = \frac{a_{0}}{ \frac{v^2}{r}} \frac{GMm}{r^2}=\frac{a_{0}}{v^2} \frac{GMm}{r}. \]

The whole point of its correct prediction is its dependency to \( 1/r \), despite the original Newton's law, which is depending on \( 1/r^2 \). If you have studied Gauss's law⁴⁴ before, you would notice that the difference between the Newton's law and Milgrom's law is that in the former we need a \( 3D \) space, and for the later we need only a \( 2D \) space, but wait! Spiral galaxies⁴⁵ are clearly \( 2D \) disks, and in above guidance to manimuchfolds we explained how to remove a dimension from a patch, so here we go! The Milgrom's law is the Newton's law, but if only you consider it in a manimuchfold of the galaxy.

The steps in above diagram, which are the boundaries as we explained, are having a kind of quantization of space-time metric field, but I have no more clue to expand it in that direction.

Pyramid Speculation

Let's move out of the serious stuff and start the fun part, which doesn't have strong evidences, but can make you think deeper. As we discussed superconductivity occurrs when matter bent, or pop, into an extra dimension, but when you see scientists are making high-temprature superconductivity⁴⁶ by increasing the pressure, we can conclude that pressure would let the matter to pop into that extra dimension. Now let's find places that have a lot of pressure. I would argue that inside the Earth's core is high pressure that could potentially force matter to pop into that extra dimension and create the superconductors. Or myabe in the comet and asteroid impacts such a hight pressure to do that job exists. But high pressure in that event is not enough! That pressure must be preserved until now in a cavity inside a strong matter. I can guess that inside some diamonds, that are created in such a high pressure environment, a high pressure cavity could still be preserved, which means if suitable materials for superconductivity existed in that environment, then inside those diamonds could potentially some superconductors exist by now. Even it's possible that the superconductivity is not activly available in those diamonds, but by adding energy through vibration or radiation to the material inside the cavity, the energy goes up enough for poping it to the extra dimension, therefore, that extra energy would push the matter to superconductivity state for the trapped molecules inside that cavity.

This model could actually exist and could potentially explain some questions. For instance, in the Earth's magnetic field⁴⁷ page in Wikipedia you can read

The Earth's magnetic field is believed to be generated by electric currents in the conductive iron alloys of its core, created by convection currents due to heat escaping from the core.

which is a declaration of some guesses about the physical origin of the Earth's magnetic field. As mentioned that it's a belief, then it's clear that that argument is not convincing. In fact, if I apply above superconductor state guess to this question, I can make more progress to answer it. Because of the pressure inside the Earth' core, the superconductor state is available, which could cause free charges inside it move around just by vibrations that are already exists by the movements and rotation of the core. This will give us a convincible magnetic field easier than iron alloys in solid state inside the core. So we could reach to a more convincible answer by applying what we learnt, but there are more answers to come.

There's another problem that I like to address here. The complete methods for construction of the Great Pyramid of Giza⁴⁸ is currently unknown, because there are very heavy granite blocks that could not be pull up to the top of pyramids without a crane machine or any other known method or tool. Also any explanation for using those tools must provide some evidence that those tools were actually existing in that period of time. This leads to some hype ideas, where I don't see any reason to avoid adding one to them. At least here I try to be rational and I'll stick to evidences.

To answer above question you may guessed that I'll use my superconductor card on it, and you are right! Due to the Meissner effect⁴, superconductors can levitate via their magnetic field⁴⁹.

This implies if the old egyptian civilization could have access to high-temprature superconductors, then they could move the big granite blocks up to the top of pyramids. So they just had a tools that we're not aware of, which made the whole thing mysterious for us, but it's not anymore! Also there's more evidences to support this hypothesis. In Pyramidion⁵⁰ page in the Wikipedia you can find

A pyramidion is the uppermost piece or capstone of an Egyptian pyramid ... A pyramidion was "covered in gold leaf to reflect the rays of the sun".

Wait! What if their sacred tool that helped them to build such a giant structures is the same thing that they loved, so they put it on the top of the pyramids?! It could be. Because diamonds are shining by themselves, but a diamonds that is embeded a superconductor could emit light just by vibration. Oh vibration! The mysterious tunnels inside the pyramids are actually good to make vibrations. People related those vibrations to the resonance frequencies of something, but this could be a better explanation. The vibration of the pyramids via moving water in those tunnels would be a good source of adding extra energy to the superconductor inside the diamonds to make them glow, just like how they described it, sun!

But where are the superconductor diamonds now? As you could guess, they have high level of levitation, so they probably left the Earth by now. However, there is a phenomena named Earthquake light⁵¹ that's not explained yet, but it can be explained by diamond superconductors that already exists in the soil of some regions, where could emit light by earthquake's vibration. So another indirect evidence, which also explains how the ancient civilizations probably have found those diamonds in the first place.

It's also worth mentioning Piri Reis map⁵². Recently, the map has been the focus because of the Antarctic coast in it. It's a map from 1513, where nobody back then had tools to visit the Antarctic coast. It's known that that coast is a copy from older maps, but somebody should have had the technology to go there and come back, then draw that map. As always, you guessed that I would argue we could use diamond superconductors as a boat to move fast over all over the Earth and map it out. This being said, with high probability there was indeed an old superconductor age in the history. Yet another superconductor age would be more glorifying. Just waiting for that to come.

This argument also potentially can explain why Mars doesn't have magnetic field, because lower mass means lower pressure than Earth in its core, which may prevent the molecules in the core to pop into the extra dimension they need for the superconductivity state.

Also there's a phenomena named Geomagnetic reversal⁵³ that could be easier justify if there are enough magnets all around the planet, not just in its core, to apply work, in the energy term, to the core's magnetic field, due to strongly enough magnetic interactions all over the place.

You cannot belive it but I still can go on! There are some videos around the internet that could not be explained by what we definitly know about our nature. Some of them are levitating glorying objects, which may move fast, zigzaggy, or even slow. Sometimes they turn off in a blink. If you ever see another one in the future please don't afraid of these objects! Aliens, who moved across the galaxy to visit Earth, can hide themselves easier than you might think, so go get that beautiful flying diamond. Just use a tool to grab it, jus in case! I promiss you will be rich. Remember I told you to get it in the first place, so consider giving me a half of your profit.

So many indirected evidences, but they are a lot, so there's some hopes for diamond superconductivity hypothesis after all!

Conclusion

This is a very wide discussions about superconductivity state of the matter. We started by theorizing type II superconductor, without any need to mentioning of the cooper pairs or any currently accapted theories. After developing the theory conceptually, and make a relationship between this model and fractional dimensions, and higher dimensions, of the space-time, we tried to make sense out of what removing a dimension means on a manimuchfold. The next step in this post was a mind shift from understanding the nature by forces to understanding the nature by geodesics and space-time curvatures. By providing some evidences that how such an understanding could simplify the calculations, we noticed there is a deep concept there. A concept that gives some ideas what quantization of the space-time means, and what's its relationship to the boundaries between mediums all over our reality. The next big step was providing a framework to solve dark matter related problems, which will lead to rejection of the dark matter hypothesis itself. And finally, we jumped on some pieces of a pazzle and connected them with our superconductor diamond idea.

Hope this post could release some dopamin for you on its roller coaster.

---

References

Cite

If you found this work useful, please consider citing:

@misc{hadilq2023Super,
    author = {{Hadi Lashkari Ghouchani}},
    note = {Published electronically at \url{https://hadilq.com/posts/superconductors-puzzle-pieces/}},
    gitlab = {Gitlab source at \href{https://gitlab.com/hadilq/hadilq.gitlab.io/-/tree/main/content/posts/2023-01-23-superconductors-puzzle-pieces}},
    title = {Superconductors' puzzle pieces},
    year={2023},
}